题目内容
已知
=(2+sinx,1),
=(2,-1),
=(sinx-3,1),
=(1,k),(x∈R,k∈R).
(Ⅰ)若
与(
+
)共线,求sinx的值.
(Ⅱ)若k的值使(
+
)⊥(
+
),试求k的取值范围.
(Ⅲ)若x∈[0,
],将函数y=
•
的图象纵坐标不变横坐标缩短为原来的
后,再向左平移
个单位得到函数f(x)的图象,试求函数f(x)的值域.
| a |
| b |
| c |
| d |
(Ⅰ)若
| a |
| b |
| c |
(Ⅱ)若k的值使(
| a |
| d |
| b |
| c |
(Ⅲ)若x∈[0,
| π |
| 2 |
| a |
| b |
| 1 |
| 2 |
| π |
| 8 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值,三角函数的图像与性质,向量与圆锥曲线
分析:(Ⅰ)根据向量的坐标利用向量的共线的充要条件求出结果.
(Ⅱ)根据向量的坐标,进一步求出向量垂直的充要条件,进一步确定k的结果.
(Ⅲ)根据向量的数量积,再根据正弦型函数的图象变换求出解析式,进一步利用函数的定义域,求出函数的值域.
(Ⅱ)根据向量的坐标,进一步求出向量垂直的充要条件,进一步确定k的结果.
(Ⅲ)根据向量的数量积,再根据正弦型函数的图象变换求出解析式,进一步利用函数的定义域,求出函数的值域.
解答:
解:(Ⅰ)已知:
=(2+sinx,1),
=(2,-1),
=(sinx-3,1)
则:
+
=(sinx-1,0)
由于
和
+
共线,
则:sinx-1=0
解得:sinx=1
(Ⅱ)由于
=(2+sinx,1),
=(2,-1),
=(sinx-3,1),
=(1,k)
则:
+
=(3+sinx,k+1),
+
=(sinx-1,0)
由于(
+
)⊥(
+
则:(3+sinx)(sinx-1)=0
所以:求得的结果与k值无关,k为任意实数.
(Ⅲ)y=
•
=2(2+sinx)-1=2sinx+3
图象纵坐标不变横坐标缩短为原来的
后,再向左平移
个单位得到函数f(x)的图象,
f(x)=2sin(2x+
)+3
由于x∈[0,
]
则:-
≤sin(2x+
)≤1
所以:3-
≤f(x)≤5
则函数的值域为:f(x)∈[3-
,5]
| a |
| b |
| c |
则:
| b |
| c |
由于
| a |
| b |
| c |
则:sinx-1=0
解得:sinx=1
(Ⅱ)由于
| a |
| b |
| c |
| d |
则:
| a |
| d |
| b |
| c |
由于(
| a |
| d |
| b |
| c) |
则:(3+sinx)(sinx-1)=0
所以:求得的结果与k值无关,k为任意实数.
(Ⅲ)y=
| a |
| b |
图象纵坐标不变横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 8 |
f(x)=2sin(2x+
| π |
| 4 |
由于x∈[0,
| π |
| 2 |
则:-
| ||
| 2 |
| π |
| 4 |
所以:3-
| 2 |
则函数的值域为:f(x)∈[3-
| 2 |
点评:本题考查的知识要点:向量共线的充要条件,向量垂直的充要条件的应用.利用正弦型函数的定义域求函数的值域.属于基础题型.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图所示,椭圆
如图所示,椭圆 如图,P是边长为a的正方形所在平面ABCD外一点,PA⊥平面ABCD,且PA=AB,E为AB上的点,是否存在点E,使平面PCE⊥平面PCD?若存在,指出点E的位置;若不存在,请说明理由.
如图,P是边长为a的正方形所在平面ABCD外一点,PA⊥平面ABCD,且PA=AB,E为AB上的点,是否存在点E,使平面PCE⊥平面PCD?若存在,指出点E的位置;若不存在,请说明理由.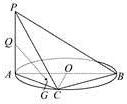 已知A,B,C是圆O上的三点,PA垂直圆O所在的平面,PB=2BC,∠PBC=60°,求证:O∈AB.
已知A,B,C是圆O上的三点,PA垂直圆O所在的平面,PB=2BC,∠PBC=60°,求证:O∈AB.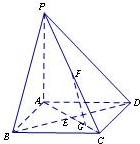 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.