题目内容
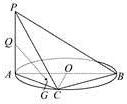 已知A,B,C是圆O上的三点,PA垂直圆O所在的平面,PB=2BC,∠PBC=60°,求证:O∈AB.
已知A,B,C是圆O上的三点,PA垂直圆O所在的平面,PB=2BC,∠PBC=60°,求证:O∈AB.考点:直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:先证明BC⊥PC,PA⊥BC即可证明BC⊥AC,从而可证AB为圆的直径,O∈AB.
解答:
证明:∵PB=2BC,∠PBC=60°,
∴BC⊥PC,
∵PA垂直圆O所在的平面,即有PA⊥BC,PA∩PC=P,
∴BC⊥平面PAC,AC?平面PAC,
∴BC⊥AC,
∴AB为圆的直径,O∈AB.
∴BC⊥PC,
∵PA垂直圆O所在的平面,即有PA⊥BC,PA∩PC=P,
∴BC⊥平面PAC,AC?平面PAC,
∴BC⊥AC,
∴AB为圆的直径,O∈AB.
点评:本题主要考察了直线与平面垂直的性质,属于基本知识的考查.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
已知椭圆的中心在原点,焦点在x轴上,椭圆的两个焦点到椭圆上的点的最大距离为3,最小距离为1,则椭圆的标准方程( )
A、
| ||||
B、
| ||||
C、x2+
| ||||
D、
|
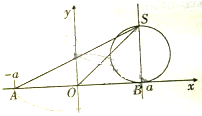 平面内与两定点A(-a,0),B(a,0)(a>0)的连线的斜率之积等于-
平面内与两定点A(-a,0),B(a,0)(a>0)的连线的斜率之积等于-