题目内容
在四面体PABC中,PA=PB=PC=AB,如果PA与平面ABC所成的角等于60°,则PC与平面PAB所成的角的最大值是 .
考点:直线与平面所成的角
专题:空间角
分析:如图所示,过点P作PO⊥平面ABC,连接OA,OB,OC.取AB的中点D,连接OD,PA.可知∠PAO是PA与平面ABC所成的角,其大小等于60°.不妨设PA=2,可得PO=
,PD=
.得到点O与D必然重合.当且仅当CD⊥AB时,PC与平面PAB所成的角取得最大值.
| 3 |
| 3 |
解答:
解:如图所示,过点P作PO⊥平面ABC,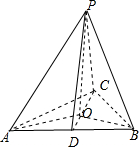
连接OA,OB,OC.取AB的中点D,连接OD,PA.
则∠PAO是PA与平面ABC所成的角,其大小等于60°.
不妨设PA=2=AB=PB=PC,则PO=
.
∴PD=
.
因此点O与D必然重合.
可知:点C在以O为圆心,AB为直径的圆周上运动(去掉A,B两点).
当且仅当CD⊥AB时,PC与平面PAB所成的角取得最大值60°.
故答案为:60°.

连接OA,OB,OC.取AB的中点D,连接OD,PA.
则∠PAO是PA与平面ABC所成的角,其大小等于60°.
不妨设PA=2=AB=PB=PC,则PO=
| 3 |
∴PD=
| 3 |
因此点O与D必然重合.
可知:点C在以O为圆心,AB为直径的圆周上运动(去掉A,B两点).
当且仅当CD⊥AB时,PC与平面PAB所成的角取得最大值60°.
故答案为:60°.
点评:本题考查了线面垂直的性质、线面角、三角形的外心性质、含30°角的直角三角形的边角关系,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
若实数x,y满足条件
则2x-y的最小值为( )
|
| A、6 | B、3 | C、0 | D、-3 |
若函数f(x)=|4x-x2|+2a-8至少有3个零点,则实数a的取值范围是( )
| A、(-∞,3) |
| B、(-∞,3] |
| C、[2,3) |
| D、[2,3] |
 设函数f(x)=x2-2|x|-3.
设函数f(x)=x2-2|x|-3.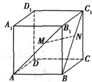 如图,在正方体ABCD-A1B1C1D1中,M、N分别是对角线AB1、BC1上的点,且
如图,在正方体ABCD-A1B1C1D1中,M、N分别是对角线AB1、BC1上的点,且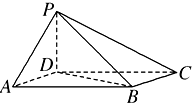 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.