题目内容
16.已知a,b,c∈R+,满足abc(a+b+c)=2,则(a+c)(b+c)的最小值是2$\sqrt{2}$.分析 由(a+c)(b+c)=ab+ac+bc+c2=ab+c(a+b+c)=ab+$\frac{2}{ab}$,由基本不等式可得.
解答 解:∵abc(a+b+c)=2,
∴$\frac{2}{abc}$=a+b+c,
∴(a+c)(b+c)=ab+ac+bc+c2=ab+c(a+b+c)=ab+$\frac{2}{ab}$≥2$\sqrt{2}$,当且仅当ab=$\sqrt{2}$时取等号,
∴(a+c)(b+c)的最小值为2$\sqrt{2}$.
故答案为:2$\sqrt{2}$
点评 本题考查基本不等式,正确变形是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.等比数列{an}中,已知a1=3,an=96,其前n顶和Sn=189,则n的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
 如图,一根长为2米的竹竿AB斜靠在在直角墙壁上,假设竹竿在同一平面内移动,当竹竿的下段点A从距离墙角O点1米的地方移动到$\sqrt{3}$米的地方,则AB的中点D经过的路程为$\frac{π}{6}$米.
如图,一根长为2米的竹竿AB斜靠在在直角墙壁上,假设竹竿在同一平面内移动,当竹竿的下段点A从距离墙角O点1米的地方移动到$\sqrt{3}$米的地方,则AB的中点D经过的路程为$\frac{π}{6}$米.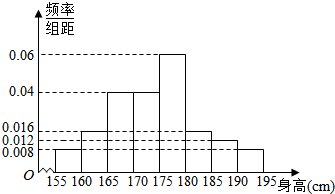 从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.
从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.