题目内容
6. 如图,一根长为2米的竹竿AB斜靠在在直角墙壁上,假设竹竿在同一平面内移动,当竹竿的下段点A从距离墙角O点1米的地方移动到$\sqrt{3}$米的地方,则AB的中点D经过的路程为$\frac{π}{6}$米.
如图,一根长为2米的竹竿AB斜靠在在直角墙壁上,假设竹竿在同一平面内移动,当竹竿的下段点A从距离墙角O点1米的地方移动到$\sqrt{3}$米的地方,则AB的中点D经过的路程为$\frac{π}{6}$米.
分析 点D的路径是:以点O为圆心,1为半径的圆弧,其圆的方程为:x2+y2=1.利用直角三角形的边角关系可得:当OA=1时,∠OAD=60°=∠DOA;当OA′=$\sqrt{3}$时,∠D′A′O=30°=∠D′OA′,可得∠DOD′=$\frac{π}{6}$.利用弧长公式即可得出.
解答 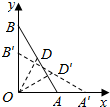 解:点D的路径是:以点O为圆心,1为半径的圆弧,其圆的方程为:x2+y2=1.
解:点D的路径是:以点O为圆心,1为半径的圆弧,其圆的方程为:x2+y2=1.
当OA=1时,∠OAD=60°=∠DOA;
当OA′=$\sqrt{3}$时,∠D′A′O=30°=∠D′OA′,
∴∠DOD′=$\frac{π}{6}$.
∴$\widehat{D{D}^{′}}$=$\frac{π}{6}$m.
故答案为:$\frac{π}{6}$.
点评 本题考查了圆的方程、直角三角形的边角关系、弧长公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知动圆M与y轴相切且与定圆A:(x-3)2+y2=9外切,则动圆的圆心M的轨迹方程是( )
| A. | y2=12x(x>0) | B. | y=0(x<0) | ||
| C. | y2=12x | D. | y2=12x(x>0)或y=0(x<0) |
1.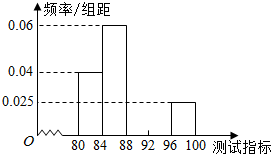 某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:
某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:
(1)试确定x,y,p.q的值,并补全频率分布直方图;
(2)为了挑选最优质的芯片,工厂决定在第三、四、五组中用分层抽样法抽取6件产品进行第二次检测,最终决定选用2件产品,求2件产品中至少有1件来自第四组的概率.
 某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:
某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:| 组号 | 测试指标 | 频数 | 频率 |
| 第一组 | [80,84] | 8 | 0.16 |
| 第二组 | [84,88] | x | 0.24 |
| 第三组 | [88,92] | 15 | p |
| 第四组 | [92,96] | 10 | q |
| 第五组 | [96,100] | y | 0.1 |
| 合 计 | 50 | 1 | |
(2)为了挑选最优质的芯片,工厂决定在第三、四、五组中用分层抽样法抽取6件产品进行第二次检测,最终决定选用2件产品,求2件产品中至少有1件来自第四组的概率.
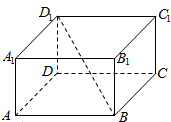 如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.
如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.