题目内容
4.已知定义在R上的偶函数f(x),当x≤0时,f(x)=$\left\{\begin{array}{l}{(x+2)^{2},x∈(-∞,-1)}\\{(\frac{1}{2})^{x}-1,x∈[-1,0]}\end{array}\right.$,则f(f(3))=( )| A. | -9 | B. | -1 | C. | 1 | D. | 9 |
分析 根据已知中函数f(x)是定义在R上的偶函数,当x≤0时,f(x)=$\left\{\begin{array}{l}{(x+2)^{2},x∈(-∞,-1)}\\{(\frac{1}{2})^{x}-1,x∈[-1,0]}\end{array}\right.$,可得f(3)=f(-3)=1,则f(f(3))=f(1)=f(-1),代入可得答案.
解答 解:∵函数f(x)是定义在R上的偶函数,当x≤0时,f(x)=$\left\{\begin{array}{l}{(x+2)^{2},x∈(-∞,-1)}\\{(\frac{1}{2})^{x}-1,x∈[-1,0]}\end{array}\right.$,
∴f(3)=f(-3)=(-3+2)2=1,
∴f(f(3))=f(1)=f(-1)=${(\frac{1}{2})}^{-1}-1$=1,
故选:C.
点评 本题考查的知识点是函数的奇偶性,分段函数的应用,函数求值,难度中档.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
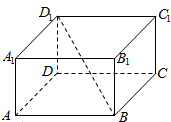 如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.
如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.