题目内容
7.求过点P(-1,3),并且在两轴上的截距相等的直线方程.分析 根据题意,分2种情况讨论:①、直线过原点,由直线过P(-1,3),分析可得直线的方程,②、直线不过原点,设直线的方程为$\frac{x}{a}$+$\frac{y}{a}$=1,将P(-1,3)代入可得$\frac{-1}{a}$+$\frac{3}{a}$=1,解可得a的值,即可得直线的方程;综合2种情况即可得答案.
解答 解:根据题意,分2种情况讨论:
①、直线过原点,此时直线在两轴上的截距都是0,
此时直线过P(-1,3),直线的方程为y=-3x;
②、直线不过原点,此时直线在两轴上的截距相等,
设直线的方程为$\frac{x}{a}$+$\frac{y}{a}$=1,
又由直线过P(-1,3),则有$\frac{-1}{a}$+$\frac{3}{a}$=1,
解可得a=2,
则直线的方程为$\frac{x}{a}$+$\frac{y}{a}$=1,即x+y=2;
故直线的方程为y=-3x和x+y=2.
点评 本题考查直线的截距式方程,注意不能忽略直线过原点的问题.

练习册系列答案
相关题目
17.已知动圆M与y轴相切且与定圆A:(x-3)2+y2=9外切,则动圆的圆心M的轨迹方程是( )
| A. | y2=12x(x>0) | B. | y=0(x<0) | ||
| C. | y2=12x | D. | y2=12x(x>0)或y=0(x<0) |
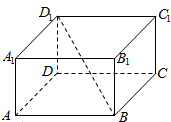 如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.
如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.