题目内容
已知△ABC满足|BC|=6,|AB|+|AC|=10,则下列命题正确的是 (写出所有正确命题的编号).
①点A的轨迹是椭圆;
②△ABC可以是以∠A为直角的直角三角形;
③△ABC面积的最大值为12;
④△ABC外接圆半径存在最小值,且为
;
⑤△ABC内切圆半径存在最大值,且为
.
①点A的轨迹是椭圆;
②△ABC可以是以∠A为直角的直角三角形;
③△ABC面积的最大值为12;
④△ABC外接圆半径存在最小值,且为
| 25 |
| 8 |
⑤△ABC内切圆半径存在最大值,且为
| 3 |
| 2 |
考点:命题的真假判断与应用
专题:阅读型,解三角形,圆锥曲线的定义、性质与方程
分析:由椭圆的定义,即可得到A的轨迹,从而判断①;
由于b>c,则以BC为直径的圆与椭圆没有交点,即可判断②;
当A为椭圆的短轴的端点,三角形ABC的面积最大,求出面积,即可判断③;
由正弦定理,可得2R=
=
,由于当A为短轴端点时,∠BAC最大,求出最小值,即可判断④;
设三角形的内切圆的半径为r,则由三角形的面积为
r(|AB|+|AC|+|BC|)=8r,
则由于△ABC面积的最大值为12,求出半径的最大值,即可判断⑤.
由于b>c,则以BC为直径的圆与椭圆没有交点,即可判断②;
当A为椭圆的短轴的端点,三角形ABC的面积最大,求出面积,即可判断③;
由正弦定理,可得2R=
| BC |
| sinA |
| 6 |
| sinA |
设三角形的内切圆的半径为r,则由三角形的面积为
| 1 |
| 2 |
则由于△ABC面积的最大值为12,求出半径的最大值,即可判断⑤.
解答:
解:对于①,由于△ABC满足|BC|=6,|AB|+|AC|=10,则由椭圆的定义,
可得A的轨迹为以B,C为焦点,焦距为6,长轴长为10的椭圆,(除去和B,C共线的两点),故①错误;
对于②,由于c=3,a=5则b=4,b>c,则以BC为直径的圆与椭圆没有交点,即不存在A,
使得△ABC是以∠A为直角的直角三角形,故②错误;
对于③,由于c=3,a=5则b=4,当A为椭圆的短轴的端点,三角形ABC的面积最大,
则有最大值为
×6×4=12,故③正确;
对于④,由正弦定理,可得2R=
=
,由于当A为短轴端点时,∠BAC最大,
此时sinA=2sin
cos
=2×
×
=
,即有R的最小值为:
=
,
则△ABC外接圆半径存在最小值,且为
,故④正确;
对于⑤,设三角形的内切圆的半径为r,则由三角形的面积为
r(|AB|+|AC|+|BC|)=8r,
则由于△ABC面积的最大值为12,则△ABC内切圆半径存在最大值,且为
,故⑤正确.
故答案为:③④⑤
可得A的轨迹为以B,C为焦点,焦距为6,长轴长为10的椭圆,(除去和B,C共线的两点),故①错误;
对于②,由于c=3,a=5则b=4,b>c,则以BC为直径的圆与椭圆没有交点,即不存在A,
使得△ABC是以∠A为直角的直角三角形,故②错误;
对于③,由于c=3,a=5则b=4,当A为椭圆的短轴的端点,三角形ABC的面积最大,
则有最大值为
| 1 |
| 2 |
对于④,由正弦定理,可得2R=
| BC |
| sinA |
| 6 |
| sinA |
此时sinA=2sin
| A |
| 2 |
| A |
| 2 |
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
| 3 | ||
|
| 25 |
| 8 |
则△ABC外接圆半径存在最小值,且为
| 25 |
| 8 |
对于⑤,设三角形的内切圆的半径为r,则由三角形的面积为
| 1 |
| 2 |
则由于△ABC面积的最大值为12,则△ABC内切圆半径存在最大值,且为
| 3 |
| 2 |
故答案为:③④⑤
点评:本题考查圆锥曲线的定义、性质和运用,考查三角形的正弦定理和面积公式的运用,考查三角函数的求值,考查推理能力,属于中档题和易错题.

练习册系列答案
相关题目
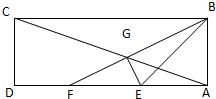 在矩形ABCD中,AB=2,AD=6,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为圆H.
在矩形ABCD中,AB=2,AD=6,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为圆H.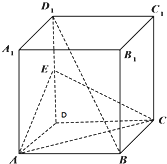 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点