题目内容
设f(x)=cos(sinx)与g(x)=sin(cosx),以下结论错误的是( )
| A、f(x)与g(x)都是偶函数 |
| B、f(x)与g(x)都是周期函数 |
| C、f(x)与g(x)的定义域都是[-1,1] |
| D、f(x)的值域是[cos1,1],g(x)的值域是[-sin1,sin1] |
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用,三角函数的图像与性质
分析:由函数的奇偶性的定义及诱导公式,即可判断A;运用函数的周期的定义和诱导公式,即可判断B;
由定义域为R,即可判断C;由正弦、余弦函数的值域和单调性,即可判断D.
由定义域为R,即可判断C;由正弦、余弦函数的值域和单调性,即可判断D.
解答:
解:对于A,定义域R关于原点对称,f(-x)=cos(sin(-x))=cos(-sinx)=cos(sinx)=f(x),
g(-x)=sin(cos(-x))=sin(cosx)=g(x),故f(x),g(x)均为偶函数,故A正确;
对于B,由于f(x+π)=cos(sin(x+π))=cos(-sinx)=cos(sinx)=f(x),故f(x)为周期为π的函数.
g(x+2π)=sin(cos(x+2π))=sin(cosx)=g(x),则g(x)是周期为2π的函数,故B正确;
对于C,f(x)与g(x)的定义域均为R,故C错误;
对于D,f(x)=cos(sinx),由于sinx∈[-1,1],则f(x)∈[cos1,1];
g(x)=sin(cosx),由于cosx∈[-1,1],且[-1,1]⊆[-
,
],则为增区间,
则有g(x)∈[-sin1,sin1],故D正确.
故选C.
g(-x)=sin(cos(-x))=sin(cosx)=g(x),故f(x),g(x)均为偶函数,故A正确;
对于B,由于f(x+π)=cos(sin(x+π))=cos(-sinx)=cos(sinx)=f(x),故f(x)为周期为π的函数.
g(x+2π)=sin(cos(x+2π))=sin(cosx)=g(x),则g(x)是周期为2π的函数,故B正确;
对于C,f(x)与g(x)的定义域均为R,故C错误;
对于D,f(x)=cos(sinx),由于sinx∈[-1,1],则f(x)∈[cos1,1];
g(x)=sin(cosx),由于cosx∈[-1,1],且[-1,1]⊆[-
| π |
| 2 |
| π |
| 2 |
则有g(x)∈[-sin1,sin1],故D正确.
故选C.
点评:本题考查三角函数的图象和性质,考查函数的周期性、单调性和值域等性质,属于中档题和易错题.

练习册系列答案
相关题目
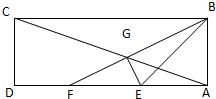 在矩形ABCD中,AB=2,AD=6,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为圆H.
在矩形ABCD中,AB=2,AD=6,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为圆H. 在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点M,N在棱CC1,BB1上,且CM=B1N,则四棱锥A-BCMN的体积为
在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点M,N在棱CC1,BB1上,且CM=B1N,则四棱锥A-BCMN的体积为