题目内容
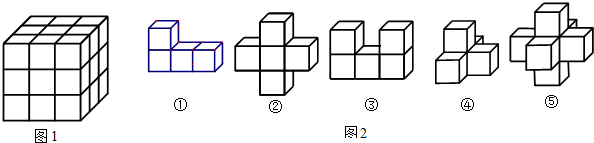
图1是一个由27个棱长为1的小正方体组成的魔方,图2是由棱长为1的小正方体组成的5种简单组合体.如果每种组合体的个数都有7个,现从总共35个组合体中选出若干组合体,使它们恰好可以拼成1个图1所示的魔方,则所需组合体的序号和相应的个数是 .(提示回答形式,如2个①和3个②,只需写出一个正确答案)

考点:简单空间图形的三视图
专题:规律型,空间位置关系与距离
分析:利用图1是一个由27个棱长为1的小正方体组成的魔方,图2是由棱长为1的小正方体组成的5种简单组合体,即可得出结论.
解答:
解:根据图1是一个由27个棱长为1的小正方体组成的魔方,图2是由棱长为1的小正方体组成的5种简单组合体,可得4个③和1个⑤可组成魔方.
故答案为:4个③和1个⑤
故答案为:4个③和1个⑤
点评:本题考查简单空间图形的三视图,比较基础.

练习册系列答案
相关题目
以下四个命题中错误的是( )
| A、已知随机变量X~N(2,9)P(X>c+1)=P(X<c+1),则c=1 | ||||
| B、两个随机变量相关性越强,则相关系数r的绝对值越接近于1 | ||||
C、在回归直线方程
| ||||
| D、对分类变量X与Y的随机变量K2的观测值k,k越小,“X与Y有关系”的把握程度越大 |
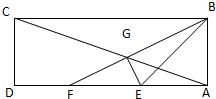 在矩形ABCD中,AB=2,AD=6,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为圆H.
在矩形ABCD中,AB=2,AD=6,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为圆H.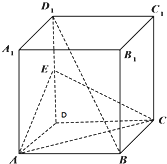 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点 在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点M,N在棱CC1,BB1上,且CM=B1N,则四棱锥A-BCMN的体积为
在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点M,N在棱CC1,BB1上,且CM=B1N,则四棱锥A-BCMN的体积为