题目内容
求证:
+
+…
≥
(
+
+…+
),
xn=1.
| 1-x1 |
| 1-x2 |
| 1-xn |
| n-1 |
| x1 |
| x2 |
| xn |
| n |
 |
| i=1 |
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:验证n=1,显然成立;当n>1时,先证一个不等式:
≥
,
设
=(
,
,…,
),
=(1,1,…,1),由|
•
|≤|
|•|
|,即可得到,即有
≥
.由于x1+x2+…+xn=1,要证原不等式成立,即证,
+
+…+
≥
(
+
+…+
).
运用上面的结论,累加即可得证.
|
| ||||||
| n |
设
| m |
| x1 |
| x2 |
| xn |
| n |
| m |
| n |
| m |
| n |
| x1+x2+…+xn |
| ||||||
|
| x2+x3+…+xn |
| x1+x3+..+xn |
| x1+x2+…+xn-1 |
| n-1 |
| x1 |
| x2 |
| xn |
运用上面的结论,累加即可得证.
解答:
证明:当n=1时,不等式左边=
=0,右边=0,显然成立;
当n>1时,先证一个不等式:
≥
,
设
=(
,
,…,
),
=(1,1,…,1),
则由于|
•
|≤|
|•|
|,
即有|
+
+…+
|≤
•
,
两边除以n,得,
≥
.
即有
≥
.
由于x1+x2+…+xn=1,
要证原不等式成立,即证,
+
+…+
≥
(
+
+…+
).
由于
≥
,
≥
,
…
≥
.
将上式累加,可得,
+
+…+
≥
=
(
+
+…+
).
故原不等式成立.
| 1-x1 |
当n>1时,先证一个不等式:
|
| ||||||
| n |
设
| m |
| x1 |
| x2 |
| xn |
| n |
则由于|
| m |
| n |
| m |
| n |
即有|
| x1 |
| x2 |
| xn |
| x1+x2+…+xn |
| n |
两边除以n,得,
|
| ||||||
| n |
即有
| x1+x2+…+xn |
| ||||||
|
由于x1+x2+…+xn=1,
要证原不等式成立,即证,
| x2+x3+…+xn |
| x1+x3+..+xn |
| x1+x2+…+xn-1 |
| n-1 |
| x1 |
| x2 |
| xn |
由于
| x2+x3+…+xn |
| ||||||
|
| x1+x3+..+xn |
| ||||||
|
…
| x1+x2+…+xn-1 |
| ||||||
|
将上式累加,可得,
| x2+x3+…+xn |
| x1+x3+..+xn |
| x1+x2+…+xn-1 |
≥
(n-1)
| ||||||
|
| n-1 |
| x1 |
| x2 |
| xn |
故原不等式成立.
点评:本题考查不等式的证明,考查向量法证明不等式的方法,考查推理能力,以及累加法,属于难题.

练习册系列答案
相关题目
函数f(x)=lnx+x-2的零点位于区间( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
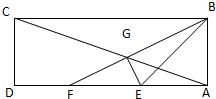 在矩形ABCD中,AB=2,AD=6,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为圆H.
在矩形ABCD中,AB=2,AD=6,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为圆H.