题目内容
△ABC的内角A、B、C对边的长a、b、c成等比数列，则
的取值范围是（ ）
| sinB+sinC |
| sinA |
| A、（0，+∞） | ||
B、（0，2+
| ||
| C、（1，+∞） | ||
D、（1，2+
|
考点：正弦定理,等比数列的通项公式
专题：解三角形
分析：设
=
=q，则由任意两边之和大于第三边求得q的范围，可得
的取值范围
| b |
| a |
| c |
| b |
| sinB+sinC |
| sinA |
解答：
解：设
=
=q，则
=
=q+q2，则由
，求得
＜q＜
，
∴
＜q2＜
，∴1＜q+q2＜2+
，
故选：D．
| b |
| a |
| c |
| b |
| sinB+sinC |
| sinA |
| b+c |
| a |
|
| ||
| 2 |
| ||
| 2 |
∴
3-
| ||
| 2 |
3+
| ||
| 2 |
| 5 |
故选：D．
点评：本题考查数列与三角函数的综合应用，是基础题．解题时要认真审题，仔细解答，注意三角形三边关系的灵活运用
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
对命题p：1∈{1}，命题q：1∉∅，下列说法正确的是（ ）
| A、p且q为假命题 |
| B、p或q为假命题 |
| C、非p为真命题 |
| D、非q为假命题 |
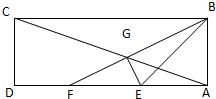在矩形ABCD中，AB=2，AD=6，E、F为AD的两个三等分点，AC和BF交于点G，△BEG的外接圆为圆H．
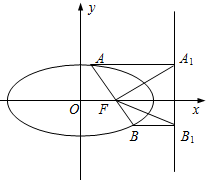已知点F为椭圆