题目内容
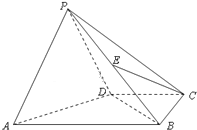 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=| 1 |
| 2 |
(Ⅰ)求证:EC∥平面APD;
(Ⅱ)求BP与平面ABCD所成角的正切值;
(Ⅲ)求二面角P-AB-D的正弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)取PA中点F,连接EF、FD,可得EF∥AB且EF=
AB,证明四边形EFDC是平行四边形,再利用直线与平面平行的判定定理进行证明;
(Ⅱ)取AD中点H,连接PH,因为PA=PD,所以PH⊥AD,可得HB是PB在平面ABCD内的射影,∠PBH是PB与平面ABCD所成角,从而求解.
(Ⅲ)在平面ABCD内过点H作AB的垂线交AB于G点,连接PG,则HG是PG在平面ABCD上的射影,故PG⊥AB,可得∠PGH是二面角P-AB-D的平面角,由AB=2a,构造直角三角形,求出∠PGH的正切值,即可求解.
| 1 |
| 2 |
(Ⅱ)取AD中点H,连接PH,因为PA=PD,所以PH⊥AD,可得HB是PB在平面ABCD内的射影,∠PBH是PB与平面ABCD所成角,从而求解.
(Ⅲ)在平面ABCD内过点H作AB的垂线交AB于G点,连接PG,则HG是PG在平面ABCD上的射影,故PG⊥AB,可得∠PGH是二面角P-AB-D的平面角,由AB=2a,构造直角三角形,求出∠PGH的正切值,即可求解.
解答:
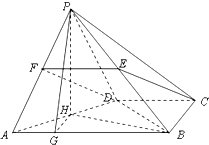 (Ⅰ)证明:如图,取PA中点F,连结EF、FD,
(Ⅰ)证明:如图,取PA中点F,连结EF、FD,
∵E是BP的中点,∴EF∥AB且EF=
AB,
又∵DC∥AB且DC=
AB,
∴EF∥DC且EF=DC,∴四边形EFDC是平行四边形,
故得EC∥FD …(2分)
又∵EC?平面PAD,FD?平面PAD,
∴EC∥平面ADE …(4分)
(Ⅱ)解:取AD中点H,连结PH,因为PA=PD,
所以PH⊥AD
∵平面PAD⊥平面ABCD于AD∴PH⊥面ABCD
∴HB是PB在平面ABCD内的射影∴∠PBH是PB与平面ABCD所成角…(6分)
∵四边形ABCD中,∠ABC=∠BCD=90°
∴四边形ABCD是直角梯形,DC=CB=
AB
设AB=2a,则BD=
a,
在△ABD中,易得∠DBA=45°,
∴AD=
a,PH=
=
a,
又∵BD2+AD2=4a2=AB2,
∴△ABD是等腰直角三角形,∠ADB=90°
∴HB=
=
a,
∴在Rt△PHB中,tan∠PBH=
=
…(10分)
(Ⅲ)解:在平面ABCD内过点H作AB的垂线交AB于G点,连结PG,
则HG是PG在平面ABCD上的射影,故PG⊥AB,
∴∠PGH是二面角P-AB-D的平面角,
由AB=2a…(11分)
∴HA=
a,
又∠HAB=45°∴HG=
a,PG=
a
在Rt△PHG中,sin∠PGH=
=
,
∴二面角P-AB-D的正弦值为
…(15分)
 (Ⅰ)证明:如图,取PA中点F,连结EF、FD,
(Ⅰ)证明:如图,取PA中点F,连结EF、FD,∵E是BP的中点,∴EF∥AB且EF=
| 1 |
| 2 |
又∵DC∥AB且DC=
| 1 |
| 2 |
∴EF∥DC且EF=DC,∴四边形EFDC是平行四边形,
故得EC∥FD …(2分)
又∵EC?平面PAD,FD?平面PAD,
∴EC∥平面ADE …(4分)
(Ⅱ)解:取AD中点H,连结PH,因为PA=PD,
所以PH⊥AD
∵平面PAD⊥平面ABCD于AD∴PH⊥面ABCD
∴HB是PB在平面ABCD内的射影∴∠PBH是PB与平面ABCD所成角…(6分)
∵四边形ABCD中,∠ABC=∠BCD=90°
∴四边形ABCD是直角梯形,DC=CB=
| 1 |
| 2 |
设AB=2a,则BD=
| 2 |
在△ABD中,易得∠DBA=45°,
∴AD=
| 2 |
| PD2-DH2 |
| ||
| 2 |
又∵BD2+AD2=4a2=AB2,
∴△ABD是等腰直角三角形,∠ADB=90°
∴HB=
| DH2+DB2 |
| ||
| 2 |
∴在Rt△PHB中,tan∠PBH=
| PH |
| HB |
| ||
| 5 |
(Ⅲ)解:在平面ABCD内过点H作AB的垂线交AB于G点,连结PG,
则HG是PG在平面ABCD上的射影,故PG⊥AB,
∴∠PGH是二面角P-AB-D的平面角,
由AB=2a…(11分)
∴HA=
| ||
| 2 |
又∠HAB=45°∴HG=
| 1 |
| 2 |
| ||
| 2 |
在Rt△PHG中,sin∠PGH=
| PH |
| PG |
| ||
| 3 |
∴二面角P-AB-D的正弦值为
| ||
| 3 |
点评:本题考查空间直线与平面位置关系的判断,空间角求解,考查空间想象能力、推理论证、计算、转化能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
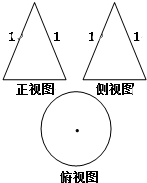 如图,一个几何体的正视图和侧视图是腰长为1的等腰三角形,俯视图是一个圆及其圆心,当这个几何体的体积最大时圆的半径是( )
如图,一个几何体的正视图和侧视图是腰长为1的等腰三角形,俯视图是一个圆及其圆心,当这个几何体的体积最大时圆的半径是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|