题目内容
已知抛物线x2=2py(p>0),过抛物线的焦点F且斜率为
的直线与抛物线交于A,B两点,与抛物线的准线交于点C(点B在线段CF上),则
= .
| 2 |
| |AF| |
| |FC| |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设直线方程为y=
x+
,代入抛物线方程,求出A,C的横坐标,即可求出
.
| 2 |
| p |
| 2 |
| |AF| |
| |FC| |
解答:
解:设直线方程为y=
x+
,代入抛物线方程,可得x2-2
px-p2=0,
∴x=(
±
)p
∴A的横坐标为(
+
)p,
又令y=-
,可得C的横坐标为-
p,
∴
=
=2+
.
故答案为:2+
.
| 2 |
| p |
| 2 |
| 2 |
∴x=(
| 2 |
| 3 |
∴A的横坐标为(
| 2 |
| 3 |
又令y=-
| p |
| 2 |
| ||
| 2 |
∴
| |AF| |
| |FC| |
| ||||
|
| 6 |
故答案为:2+
| 6 |
点评:本题考查直线与抛物线的位置关系,考查学生的计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、32 | ||
B、
| ||
| C、48 | ||
| D、64 |
i为虚数单位,则(
)2014=( )
| 1-i |
| 1+i |
| A、-i | B、-1 | C、i | D、1 |
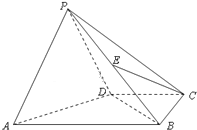 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
 如图中的程序框图所描述的算法为欧几里得辗转相除法,若输入m=11077,n=2014,则输出m=
如图中的程序框图所描述的算法为欧几里得辗转相除法,若输入m=11077,n=2014,则输出m=