题目内容
已知函数f(x)=ex-ax-1(e为自然对数的底数).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当a>0时,若f(x)≥0对任意的x∈R恒成立,求实数a的值;
(Ⅲ)求证:ln[1+
]+ln[1+
]+…+ln[1+
]<2.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当a>0时,若f(x)≥0对任意的x∈R恒成立,求实数a的值;
(Ⅲ)求证:ln[1+
| 2×3 |
| (3-1)2 |
| 2×32 |
| (32-1)2 |
| 2×3n |
| (3n-1)2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:
分析:(Ⅰ)求导数,利用导数的正负,即可求函数f(x)的单调区间;
(Ⅱ)若f(x)≥0对任意的x∈R恒成立,a-alna-1≥0对a>0恒成立,即可求实数a的值;
(Ⅲ)方法一:要证原不等式成立,只需证:
<2,即证:
<1;方法二:n≥2时,
<
=
=
-
,即可证明结论成立.
(Ⅱ)若f(x)≥0对任意的x∈R恒成立,a-alna-1≥0对a>0恒成立,即可求实数a的值;
(Ⅲ)方法一:要证原不等式成立,只需证:
| n |
 |
| k=1 |
| 2×3k |
| (3k-1)2 |
| n |
 |
| k=1 |
| 3k |
| (3k-1)2 |
| 2×3n |
| (3n-1)2 |
| 2×3n |
| (3n-1)(3n-3) |
| 2×3n-1 |
| (3n-1)(3n-1-1) |
| 1 |
| 3n-1-1 |
| 1 |
| 3n-1 |
解答:
(Ⅰ)解:f′(x)=ex-a(1分)
∴a≤0时,f′(x)>0,f(x)在R上单调递增. (2分)
a>0时,x∈(-∞,lna)时,f′(x)<0,f(x)单调递减,x∈(lna,+∞)时,f′(x)>0,f(x)单调递增.(4分)
(Ⅱ)解:由(Ⅰ),a>0时,f(x)min=f(lna),∴f(lna)≥0(5分)
即a-alna-1≥0,记g(a)=a-alna-1(a>0)∵g′(a)=1-(lna+1)=-lna∴g(a)在(0,1)上增,在(1,+∞)上递减∴g(a)≤g(1)=0
故g(a)=0,得a=1(18分)
(Ⅲ)证明:方法一:由(Ⅱ)ex≥x+1,即ln(1+x)≤x(x>-1),则x>0时,ln(1+x)<x
要证原不等式成立,只需证:
<2,即证:
<1
下证
≤
-
①(9分)
?
≤
?4(32k-2•3k+1)≥3•32k-4•3k+1?32k-4•3k+3≥0?(3k-1)(3k-3)≥0
①中令k=1,2,…,n,各式相加,得
<(
-
)+(
-
)+…+(
-
)=
-
<1成立,
故原不等式成立. (14分)
方法二:n=1时,
=
,
n≥2时,
<
=
=
-
,
n≥2时,
<
+
-
<2
∴a≤0时,f′(x)>0,f(x)在R上单调递增. (2分)
a>0时,x∈(-∞,lna)时,f′(x)<0,f(x)单调递减,x∈(lna,+∞)时,f′(x)>0,f(x)单调递增.(4分)
(Ⅱ)解:由(Ⅰ),a>0时,f(x)min=f(lna),∴f(lna)≥0(5分)
即a-alna-1≥0,记g(a)=a-alna-1(a>0)∵g′(a)=1-(lna+1)=-lna∴g(a)在(0,1)上增,在(1,+∞)上递减∴g(a)≤g(1)=0
故g(a)=0,得a=1(18分)
(Ⅲ)证明:方法一:由(Ⅱ)ex≥x+1,即ln(1+x)≤x(x>-1),则x>0时,ln(1+x)<x
要证原不等式成立,只需证:
| n |
 |
| k=1 |
| 2×3k |
| (3k-1)2 |
| n |
 |
| k=1 |
| 3k |
| (3k-1)2 |
下证
| 3k |
| (3k-1)2 |
| 2 |
| 3k-1 |
| 2 |
| 3k+1-1 |
?
| 3k |
| 32k-2•3k+1 |
| 4•3k |
| 3•32k-4•3k+1 |
?4(32k-2•3k+1)≥3•32k-4•3k+1?32k-4•3k+3≥0?(3k-1)(3k-3)≥0
①中令k=1,2,…,n,各式相加,得
| n |
 |
| k=1 |
| 3k |
| (3k-1)2 |
| 2 |
| 31-1 |
| 2 |
| 32-1 |
| 2 |
| 32-1 |
| 2 |
| 33-1 |
| 2 |
| 3n-1 |
| 2 |
| 3n+1-1 |
| 2 |
| 31-1 |
| 2 |
| 3n+1-1 |
故原不等式成立. (14分)
方法二:n=1时,
| 2×3n |
| (3n-1)2 |
| 3 |
| 2 |
n≥2时,
| 2×3n |
| (3n-1)2 |
| 2×3n |
| (3n-1)(3n-3) |
| 2×3n-1 |
| (3n-1)(3n-1-1) |
| 1 |
| 3n-1-1 |
| 1 |
| 3n-1 |
n≥2时,
| n |
 |
| k=1 |
| 3k |
| (3k-1)2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3n-1 |
点评:本题考查导数知识的运用,考查函数的单调性,函数的最值,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设等差数列{an}的前n项和为Sn,若9S5+5S9=90,则S7=( )
| A、7 | B、14 | C、21 | D、22 |
已知函数f(x)=3sin(2x-
),则下列结论正确的是( )
| π |
| 4 |
| A、若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | ||||
B、函数f(x)的图象与g(x)=3cos(2x+
| ||||
C、函数f(x)的图象关于(-
| ||||
D、函数f(x)在区间[-
|
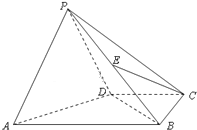 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=