题目内容
设函数f(x)=2sinφcos2x+cosφsin2x-sinφ(0<φ<π)在x=
时取得最大值.
(1)求函数f(x)的解析式及最小正周期;
(2)若函数g(x)的图象与函数f(x)的图象关于直线x=
对称,求函数g(x)的单调递增区间.
| π |
| 6 |
(1)求函数f(x)的解析式及最小正周期;
(2)若函数g(x)的图象与函数f(x)的图象关于直线x=
| π |
| 12 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)由二倍角的余弦公式及两角和的正弦公式化简,再由在x=
时取得最大值,结合φ得范围求得φ,则函数解析式可求;
(2)设出函数g(x)的图象上的点的坐标,由对称性求得函数g(x)的解析式,再由复合函数的单调性求得函数g(x)的单调递增区间.
| π |
| 6 |
(2)设出函数g(x)的图象上的点的坐标,由对称性求得函数g(x)的解析式,再由复合函数的单调性求得函数g(x)的单调递增区间.
解答:
解:(1)f(x)=2sinφcos2x+cosφsin2x-sinφ
=sinφ(1+cos2x)+cosφsin2x-sinφ
=sin2xcosφ+cos2xsinφ=sin(2x+φ).
∵x=
时f(x)求得最大值,
∴2×
+φ=2kπ+
,即φ=2kπ+
.
又因0<φ<π,所以=
.
于是函数f(x)的解析式为f(x)=sin(2x+
),其最小正周期为π;
(2)设(x,y)是函数g(x)图象上任一点,
则其关于直线x=
的对称点为(
-x,y),该点在函数f(x)的图象上,
∴y=sin[2(
-x)+
]=sin(
-2x)=cos2x,
于是g(x)=cos2x.
由2kπ-π≤2x≤2kπ,解得kπ-
≤x≤kπ,k∈Z.
∴函数g(x)的单调递增区间为[kπ-
,kπ](k∈Z).
=sinφ(1+cos2x)+cosφsin2x-sinφ
=sin2xcosφ+cos2xsinφ=sin(2x+φ).
∵x=
| π |
| 6 |
∴2×
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
又因0<φ<π,所以=
| π |
| 6 |
于是函数f(x)的解析式为f(x)=sin(2x+
| π |
| 6 |
(2)设(x,y)是函数g(x)图象上任一点,
则其关于直线x=
| π |
| 12 |
| π |
| 6 |
∴y=sin[2(
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
于是g(x)=cos2x.
由2kπ-π≤2x≤2kπ,解得kπ-
| π |
| 2 |
∴函数g(x)的单调递增区间为[kπ-
| π |
| 2 |
点评:本题考查三角函数的图象及图象变换,考查了三角函数的倍角公式及两角和的正弦,训练了复合函数的单调性的求法,是中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
设集合M={-1,1},N={a2},则“a=1”是“M∪N=M”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
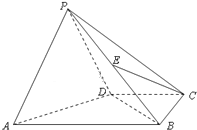 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=