题目内容
设函数f(x)=
(e=2.71828…是自然对数的底数).
(1)求f(x)的单调区间及最大值;
(2)?x∈(0,+∞),2|lnx-ln2|≥f(x)+c恒成立,试求实数c的取值范围.
| x |
| ex |
(1)求f(x)的单调区间及最大值;
(2)?x∈(0,+∞),2|lnx-ln2|≥f(x)+c恒成立,试求实数c的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)求导数,利用导数的正负,即可求函数f(x)的单调区间,从而可得函数的最大值;
(2)由?x∈(0,+∞),2|lnx-ln2|≥f(x)+c恒成立,可知?x∈(0,+∞),2|lnx-ln2|-f(x)≥c恒成立,构造函数g(x)=2|lnx-ln2|-f(x)=2|lnx-ln2|-
,分类讨论,确定函数的单调性,求最值,即可求实数c的取值范围.
(2)由?x∈(0,+∞),2|lnx-ln2|≥f(x)+c恒成立,可知?x∈(0,+∞),2|lnx-ln2|-f(x)≥c恒成立,构造函数g(x)=2|lnx-ln2|-f(x)=2|lnx-ln2|-
| x |
| ex |
解答:
解:(1)f′(x)=
由f'(x)=0,解得x=1
当x<1,时f'(x)>0,f(x)单调递增;
当x>1,时f'(x)<0,f(x)单调递减.
所以,函数f(x)的单调递增区间是(-∞,1),单调递减区间是(1,+∞),其最大值为f(1)=
(2)由?x∈(0,+∞),2|lnx-ln2|≥f(x)+c恒成立
可知?x∈(0,+∞),2|lnx-ln2|-f(x)≥c恒成立
令g(x)=2|lnx-ln2|-f(x)=2|lnx-ln2|-
①当x>2时g(x)=2(lnx-ln2)-
所以g′(x)=
-
=
>0
因此g(x)在(2,+∞)上单调递增
②当0<x<2时g(x)=2(ln2-lnx)-
所以g′(x)=-
-
=-
因为0<x<2,所以2ex>2,x(1-x)=-(x-
)2+
∈(-2,
)
所以2ex+x(1-x)>0,
所以g′(x)<0,
因此g(x)在(0,2)上单调递减
综上①②可知g(x)在x=2时取得最小值g(2)=-
因为?x∈(0,+∞),2|lnx-ln2|-f(x)≥c即g(x)≥c恒成立
所以c≤-
.
| 1-x |
| ex |
由f'(x)=0,解得x=1
当x<1,时f'(x)>0,f(x)单调递增;
当x>1,时f'(x)<0,f(x)单调递减.
所以,函数f(x)的单调递增区间是(-∞,1),单调递减区间是(1,+∞),其最大值为f(1)=
| 1 |
| e |
(2)由?x∈(0,+∞),2|lnx-ln2|≥f(x)+c恒成立
可知?x∈(0,+∞),2|lnx-ln2|-f(x)≥c恒成立
令g(x)=2|lnx-ln2|-f(x)=2|lnx-ln2|-
| x |
| ex |
①当x>2时g(x)=2(lnx-ln2)-
| x |
| ex |
所以g′(x)=
| 2 |
| x |
| 1-x |
| ex |
| 2ex+x(x-1) |
| xex |
因此g(x)在(2,+∞)上单调递增
②当0<x<2时g(x)=2(ln2-lnx)-
| x |
| ex |
所以g′(x)=-
| 2 |
| x |
| 1-x |
| ex |
| 2ex+x(1-x) |
| xex |
因为0<x<2,所以2ex>2,x(1-x)=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
所以2ex+x(1-x)>0,
所以g′(x)<0,
因此g(x)在(0,2)上单调递减
综上①②可知g(x)在x=2时取得最小值g(2)=-
| 2 |
| e2 |
因为?x∈(0,+∞),2|lnx-ln2|-f(x)≥c即g(x)≥c恒成立
所以c≤-
| 2 |
| e2 |
点评:本题考查导数知识的综合运用,考查函数的单调性,考查恒成立问题,正确求导,求最值是关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知函数f(x)=3sin(2x-
),则下列结论正确的是( )
| π |
| 4 |
| A、若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | ||||
B、函数f(x)的图象与g(x)=3cos(2x+
| ||||
C、函数f(x)的图象关于(-
| ||||
D、函数f(x)在区间[-
|
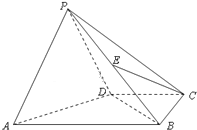 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
 如图中的程序框图所描述的算法为欧几里得辗转相除法,若输入m=11077,n=2014,则输出m=
如图中的程序框图所描述的算法为欧几里得辗转相除法,若输入m=11077,n=2014,则输出m=