题目内容
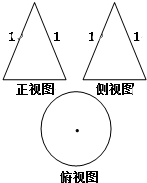 如图,一个几何体的正视图和侧视图是腰长为1的等腰三角形,俯视图是一个圆及其圆心,当这个几何体的体积最大时圆的半径是( )
如图,一个几何体的正视图和侧视图是腰长为1的等腰三角形,俯视图是一个圆及其圆心,当这个几何体的体积最大时圆的半径是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:由三视图求面积、体积
专题:不等式的解法及应用,空间位置关系与距离
分析:几何体是圆锥,且圆锥的母线长为1,设底面半径为R,构造以R为自变量的函数,并利用基本不等式求函数的最值,判断取到“=”的条件可得答案.
解答:
解:由三视图知:几何体是圆锥,且圆锥的母线长为1,
设底面半径为R,则圆锥的体积V=
π×R2×
=
π×
×
≤
π×
=
π,
当R2=2-2R2时,即R=
,取“=”,
故选:C.
设底面半径为R,则圆锥的体积V=
| 1 |
| 3 |
| 1-R2 |
| 1 |
| 3 |
| ||
| 2 |
| R2R2(2-2R2) |
| ||
| 6 |
|
2
| ||
| 27 |
当R2=2-2R2时,即R=
| ||
| 3 |
故选:C.
点评:本题结合三视图考查了圆锥的体积最大值问题,考查了学生的运算能力,根据几何体的结构特征构造以R为变量的函数,并利用基本不等式求函数的最值是解答本题的关键.

练习册系列答案
相关题目
已知平面向量
=(1,2),
=(2,m),且
∥
,则3
+2
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、(7,2) |
| B、(7,14) |
| C、(7,-4) |
| D、(7,-8) |
设等差数列{an}的前n项和为Sn,若9S5+5S9=90,则S7=( )
| A、7 | B、14 | C、21 | D、22 |
设复数z1=1+i,z2=2+bi,若z1•z2为纯虚数,则实数b=( )
| A、2 | B、-2 | C、1 | D、-1 |
 已知a为如图所示的程序框图输出的结果,则二项式(a
已知a为如图所示的程序框图输出的结果,则二项式(a| x |
| 1 | ||
|
| A、-20 | ||
B、
| ||
| C、-192 | ||
| D、-160 |
设集合M={-1,1},N={a2},则“a=1”是“M∪N=M”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
已知函数f(x)=3sin(2x-
),则下列结论正确的是( )
| π |
| 4 |
| A、若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | ||||
B、函数f(x)的图象与g(x)=3cos(2x+
| ||||
C、函数f(x)的图象关于(-
| ||||
D、函数f(x)在区间[-
|
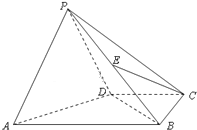 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=