题目内容

已知f（x）=sin（2x+
π
3
）+1，x∈R．
（1）求函数f（x）的最小正周期；
（2）求函数f（x）的单调增区间．
考点：函数y=Asin（ωx+φ）的图象变换,三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：（1）利用正弦函数的周期公式即可求得答案；
（2）利用正弦函数的单调性，解不等式2kπ-
π
2
≤2x+
π
3
≤2kπ+
π
2
，k∈Z．即可求得其单调增区间．
解答： 解：（1）∵f（x）=sin（2x+
π
3
）+1，
∴f（x）的最小正周期T=
2π
2
=π；
（2）由2kπ-
π
2
≤2x+
π
3
≤2kπ+
π
2
，k∈Z．
得：kπ-
5π
12
≤x≤kπ+
π
12
，k∈Z．
∴f（x）的单调增区间为[kπ-
5π
12
，kπ+
π
12
]，k∈Z．
点评：本题考查三角函数的周期性及其求法，考查正弦函数的单调性，属于基础题．
练习册系列答案
相关题目
已知a为如图所示的程序框图输出的结果，则二项式（a
x
-
1
x
）6的展开式中常数项是（　　）
A、-20
B、
5
2
C、-192
D、-160
已知函数f（x）=lnx-a（x-1），g（x）=ex．
（Ⅰ）若a=2，设h（x）=f（x+1）+g（x），当x≥0时，求h（x）的最小值；
（Ⅱ）过原点分别作函数f（x）与g（x）的切线，且两切线的斜率互为倒数，证明：a=0或1＜a＜2．
已知函数f（x）=2lnx-ax+a（a∈R）．
（1）如果曲线y=f（x）在（1，0）处的切线恰与直线y=x平行，求a的值；
（2）讨论f（x）的单调性；
（3）若f（x）≤0恒成立，证明：当0＜x1＜x2时，
f(x2)-f(x1)
x2-x1
＜2（
1
x2
-1）．
在△ABC中，角A，B，C所对的边分别为a，b，c，且cosA=
2
3
．
（Ⅰ）求2cos2
B+C
2
+sin2（B+C）；
（Ⅱ）若a=
3
，求△ABC面积的最大值．
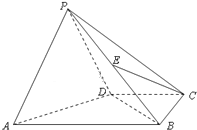如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，∠ABC=∠BCD=90°，PA=PD=DC=CB=
1
2
AB，E是BD的中点．
（Ⅰ）求证：EC∥平面APD；
（Ⅱ）求BP与平面ABCD所成角的正切值；
（Ⅲ）求二面角P-AB-D的正弦值．
已知函数f（x）=2sin2x-2sinxcos（x+
π
2
）．
（1）求函数f（x）的最小正周期；
（2）求函数f（x）在区间[0，
π
2
]上的值域．
（
5x
-
1
x
）12的展开式中的常数项为
 
．
设变量x、y满足约束条件
y-1≥0
x+y-4≤0
y-1≤k(x-1)
，其中k∈R，k＞0，
（1）当k=1时，
y-1
x+1
的最大值为
 
；
（2）若
y-1
x+1
的最大值为
1
2
，则实数k的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网