题目内容
角2013°的弧度表示为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：弧度与角度的互化
专题：三角函数的求值
分析：根据180°与π相等的关系，写出一度对应的代数式，用120乘以一度对应的代数式，求出结果，不要漏掉负号．
解答：
解：∵2013°=2013×
=
π，
∴2013°化为弧度为
π，
故选：B．
| π |
| 180 |
| 671 |
| 60 |
∴2013°化为弧度为
| 671 |
| 60 |
故选：B．
点评：本题考查弧度与角度的互化，本题解题时，要用180°和π的关系．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
如图，AB是半圆O的直径，C在半圆上，CD⊥AB于点D，且AD=3DB，AE=EO，设∠CED=θ，则tan2θ=设O为△ABC的外心，且
+
+
=
，|
|=1则
•（
+
）值是（ ）
| OA |
| OB |
| 3 |
| OC |
| 0 |
| AB |
| CO |
| CA |
| CB |
A、2-
| ||
| B、2 | ||
C、2+
| ||
| D、4 |
已知向量
=（cos
，sin
），
=（-1，0）．则向量
与
的夹角为（ ）
| a |
| π |
| 6 |
| π |
| 6 |
| b |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、
|
如图，在正方体ABCD-A1B1C1D1中，M，N分别是BC1，CD1的中点，则下列说法错误的是（ ）
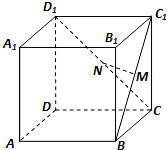
| A、MN与AB1平行 |
| B、MN与CC1垂直 |
| C、MN与AC垂直 |
| D、MN与BD平行 |
已知复数z=cosθ+isinθ（0≤θ＜π），则使z2=-1的θ的值为（ ）
| A、0 | ||
B、
| ||
C、
| ||
D、
|
设曲线C：x2=y上有两个动点A、B，直线AB与曲线C在A点处切线垂直，则点B到y轴距离的最小值是（ ）
A、2
| ||
B、
| ||
C、
| ||
| D、2 |
在一次物理实验课上，某同学在弹性限度范围内，将弹簧劲度系数为60N/m的一弹簧从平衡位置拉到离开平衡位置的
m处，则该同学克服弹力所做的功为（ ）
| 1 |
| 4 |
| A、15 | ||
B、
| ||
C、
| ||
D、
|
设直线ax+by+c=0的倾斜角为θ（θ≠0，θ≠
），且sinθ-cosθ=0，则a、b满足（ ）
| π |
| 2 |
| A、a+b=1 |
| B、a-b=1 |
| C、a+b=0 |
| D、a-b=0 |