题目内容
如图，在正方体ABCD-A1B1C1D1中，M，N分别是BC1，CD1的中点，则下列说法错误的是（ ）
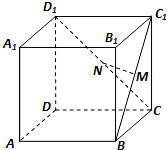
| A、MN与AB1平行 |
| B、MN与CC1垂直 |
| C、MN与AC垂直 |
| D、MN与BD平行 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：先利用三角形中位线定理证明MN∥BD，再利用线面垂直的判定定理定义证明MN与CC1垂直，由异面直线所成的角的定义证明MN与AC垂直，故排除B、C、D选A．
解答：
解：如图：连接C1D，BD，
在三角形C1DB中，MN∥BD，故D正确；
∵CC1⊥平面ABCD，
∴CC1⊥BD，∴MN与CC1垂直，故B正确；
∵AC⊥BD，MN∥BD，
∴MN与AC垂直，故C正确；
∵AB1与BD异面，MN∥BD，
∴MN与AB1不可能平行，故A错误
故选：A．
解：如图：连接C1D，BD，在三角形C1DB中，MN∥BD，故D正确；
∵CC1⊥平面ABCD，
∴CC1⊥BD，∴MN与CC1垂直，故B正确；
∵AC⊥BD，MN∥BD，
∴MN与AC垂直，故C正确；
∵AB1与BD异面，MN∥BD，
∴MN与AB1不可能平行，故A错误
故选：A．
点评：本题主要考查了正方体中的线面关系，线线平行与垂直的证明，异面直线所成的角及其位置关系，熟记正方体的性质是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
定义平面向量之间的一种运算“⊙”如下：对任意向量
=（x1，y1），
=（x2，y2），令
⊙
=x1y2-x2y1，则下列说法中错误的是（ ）
| a |
| b |
| a |
| b |
A、2
| ||||||||
B、
| ||||||||
C、|
| ||||||||
D、若
|
已知
，
满足：|
|=3，|
|=4，|
-
|=5，则|
+
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、3 | ||
B、
| ||
| C、5 | ||
| D、4 |
若函数f（x）=
-
+ln3的导函数为f′（x），则f′（x）=（ ）
| x |
| 1 |
| x |
A、f′（x）=
| ||||||||
B、f′（x）=
| ||||||||
C、f′（x）=
| ||||||||
D、f′（x）=
|
角2013°的弧度表示为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
极坐标方程ρ=sin（θ+3）（θ为参数）表示的曲线是（ ）
| A、双曲线 | B、椭圆 | C、抛物线 | D、圆 |
已知函数f（x）=aln（x+
）+bsinx+1满足f（2）=3，则f（-2）等于（ ）
| x2+1 |
| A、-3 | B、-1 | C、0 | D、1 |