题目内容
10.已知等差数列{an}的首项为1,前n项和为Sn,且S1,S3,S9成等比数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记Tn为数列{$\frac{1}{{a}_{n+1}{a}_{n}}$}的前n项和,求Tn.
分析 (Ⅰ)通过设数列{an}的公差为d,利用S1,S3,S9成等比数列可知(3+3d)2=9+36d,解出d的值,进而可得结论;
(Ⅱ)通过(I)可知,当an=1时Tn=n;当an=2n-1时,裂项、并项相加即得结论.
解答 解:(Ⅰ)设数列{an}的公差为d,则(3+3d)2=9+36d,
即d(d-2)=0,∴d=0或d=2,
当d=0时,an=1;
当d=2时,an=2n-1;
(Ⅱ)由(I)可知,当an=1时,Tn=n;
当an=2n-1时,Tn=$\frac{1}{1×3}$+$\frac{1}{3×5}$+…+$\frac{1}{(2n-1)(2n+1)}$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)
=$\frac{n}{2n+1}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,考查分类讨论的思想,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
1.甲、乙两个粮库要项A,B量诊运送大米,已知甲库将调出100吨大米,乙库将调出80吨大米,A镇至少需要60吨大米,B镇至少需要100吨大米,且甲往B镇运送大米的吨数不少于乙往A镇运送大米的吨数的2倍,两库到两镇运费如表(其中a为常数,$\frac{1}{2}$<a<2).
为了满足上述要求,同时使总运费最省,试问甲、乙粮库应运往A镇各多少吨大米?
| 运费(元/吨) | ||
| 甲库 | 乙库 | |
| A镇 | 240+10a | 180 |
| B镇 | 260 | 210 |
15.f(x)是定义在(0,+∞)上的函数,满足3f(x)-xf′(x)<0,下列正确的是( )
| A. | $\sqrt{2}$f(2)<4f($\sqrt{2}$) | B. | $\sqrt{2}$f(2)>4f($\sqrt{2}$) | ||
| C. | $\sqrt{2}$f(2)=4f($\sqrt{2}$) | D. | 两者大小关系无法确定 |
19.在一定的储存温度范围内,某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系y=ekx+b(e=2.71828…为自然对数的底数,k、b为常数).若该食品在0℃的保鲜时间为200小时,在30℃的保鲜时间是25小时,则该食品在20℃的保鲜时间是( )
| A. | 40小时 | B. | 50小时 | C. | 60小时 | D. | 80小时 |
20.直线2(m+1)x+(m-3)y-5m-1=0与圆(x-1)2+y2=3的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法判断 |
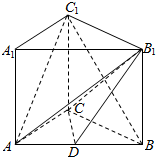 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=4,BC=3,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=4,BC=3,AB=5,AA1=4,点D是AB的中点.