题目内容
20.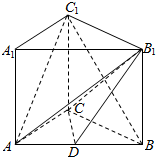 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=4,BC=3,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=4,BC=3,AB=5,AA1=4,点D是AB的中点.(1)求证:AC1∥平面CDB1;
(2)求直线AB1与平面BB1C1C所成角的正切值.
分析 (1)设BC1∩CB1于点O,连结OD,则OD$\underset{∥}{=}$$\frac{1}{2}$$\overrightarrow{A{C}_{1}}$,由此能证明AC1∥平面CDB1.
(2)推导出AC⊥BC,AC⊥C1C,从而∠AB1C是直线AB1与平面B1BCC1所成角,由此能求出直线AB1与平面BB1C1C所成角的正弦值.
解答 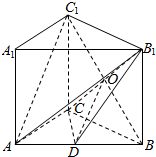 证明:(1)如图,设BC1∩CB1于点O,连结OD,
证明:(1)如图,设BC1∩CB1于点O,连结OD,
∵O、D分别是BC1和AB的中点,∴OD$\underset{∥}{=}$$\frac{1}{2}$$\overrightarrow{A{C}_{1}}$,
又∵OD?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
(2)∵AC=4,BC=3,AB=5,∴∠ACB=90°,即AC⊥BC,
在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,∴AC⊥C1C,
又BC∩CC1=C,∴AC⊥平面BCC1B1,
∴直线B1C是斜线AB1在平面B1BCC1上的射影,
∴∠AB1C是直线AB1与平面B1BCC1所成角,
在Rt△AB1C中,B1C=5,AC=4,
∴tan∠AB1C=$\frac{4}{5}$,
即直线AB1与平面BB1C1C所成角的正弦值为$\frac{4}{5}$.
点评 本题考查线面平行的证明,考查直线面角的正弦值的求法,是中档题,解题时要认真审题,注意综合法的合理运用.

练习册系列答案
相关题目
10.已知直线l:x+y-4=0,定点P(2,0),E,F分别是直线l和y轴上的动点,则△PEF的周长的最小值为( )
| A. | 2$\sqrt{10}$ | B. | 6 | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{5}$ |
11.“2<m<6”是“方程(6-m)x2+(m-2)y2=-m2+8m-12表示椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.给出下列四个命题:①没有公共点的两条直线平行;②互相垂直的两条直线是相交直线;③既不平行也不相交的两条直线是异面直线;④不同在任何一个平面内的两条直线是异面直线.
其中正确的命题是( )
其中正确的命题是( )
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
12.已知f(x)是定义在R上的函数,且满足①f(4)=0;②曲线y=f(x+1)关于点(-1,0)对称;③x∈(-4,0)时,f(x)=log2($\frac{x}{{e}^{|x|}}$+ex-m).若y=f(x)在x∈[-4,4]上恰有7个零点,则实数m的取值范围为( )
| A. | (-∞,-e-2) | B. | (-1-e-2,-e-2) | C. | (-1-e-2,0) | D. | (-1-e-2,-1-3e-4) |