题目内容
19．在一定的储存温度范围内，某食品的保鲜时间y（单位：小时）与储存温度x（单位：℃）满足函数关系y=ekx+b（e=2.71828…为自然对数的底数，k、b为常数）．若该食品在0℃的保鲜时间为200小时，在30℃的保鲜时间是25小时，则该食品在20℃的保鲜时间是（ ）| A． | 40小时 | B． | 50小时 | C． | 60小时 | D． | 80小时 |
分析 由题意得$\left\{\begin{array}{l}{200={e}^{b}}\\{25={e}^{30k+b}}\end{array}\right.$，从而可得e30k=$\frac{1}{8}$，而e20k=$（{e}^{30k}）^{\frac{2}{3}}$，从而解得．
解答 解：由题意得，
$\left\{\begin{array}{l}{200={e}^{b}}\\{25={e}^{30k+b}}\end{array}\right.$，
故e30k=$\frac{25}{200}$=$\frac{1}{8}$，
故e20k+b=e20k•eb
=$（\frac{1}{8}）^{\frac{2}{3}}$×200=50，
故选：B．
点评 本题考查了指数函数的变形应用及指数运算的应用．
练习册系列答案
相关题目
7．
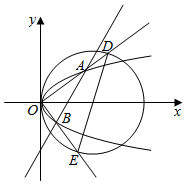如图所示，过点（1，0）的直线与抛物线y2=x交于A、B两点，射线OA和OB分别和圆（x-2）2+y2=4交于D、E两点，若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ，则λ的最小值是（ ）
如图所示，过点（1，0）的直线与抛物线y2=x交于A、B两点，射线OA和OB分别和圆（x-2）2+y2=4交于D、E两点，若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ，则λ的最小值是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
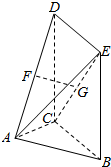如图，平面DCBE⊥平面ABC，四边形DCBE为矩形，且BC=$\sqrt{2}$AB=$\sqrt{2}$AC，F、G分别为AD、CE的中点．
11．不等式$\frac{2-x}{1+x}$≥0的解集为（ ）
| A． | （-1，2] | B． | [-1，2] | C． | （-∞，-1）∪（2，+∞） | D． | （-∞，-1]∪（2，+∞） |
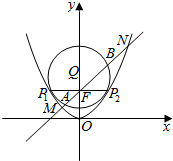如图，抛物线C：x2=2py（p＞0）的焦点为F（0，1），取垂直于y轴的直线与抛物线交于不同的两点P1，P2．过P1，P2作圆心为Q的圆，使抛物线的其余点均在圆外，且P1Q⊥P2Q．