题目内容
2.已知圆C过点(2,0),且圆心在x轴的正半轴上,直线l:x+y-7=0被该圆所截得的弦长为2$\sqrt{7}$,则圆C的标准方程为(x-5)2+y2=9.分析 根据题意,设圆心为C(a,b),算出点C到直线x+y-7=0的距离,根据垂径定理建立方程,由于圆C过点(2,0),所以(2-a)2+(0-b)2=r2,又因为圆心在x轴的正半轴上,则b=0,即可得到所求圆的方程.
解答 解:设所求的圆的方程是(x-a)2+(y-b)2=r2,
则圆心(a,b)到直线x+y-7=0的距离为$\frac{|a+b-7|}{\sqrt{2}}$,
所以($\frac{|a+b-7|}{\sqrt{2}}$)2+7=r2,-------①
由于圆C过点(2,0),所以(2-a)2+(0-b)2=r2-----------②
又因为圆心在x轴的正半轴上,则b=0---------③
联立①②③,a>0,解得a=5,b=0,r2=9
∴所求的圆的方程是(x-5)2+y2=9.
故答案为:(x-5)2+y2=9.
点评 本题给出圆满足的条件,求圆的方程.着重考查了圆的标准方程、点到直线的距离公式、直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
12.已知f(x)是定义在R上的函数,且满足①f(4)=0;②曲线y=f(x+1)关于点(-1,0)对称;③x∈(-4,0)时,f(x)=log2($\frac{x}{{e}^{|x|}}$+ex-m).若y=f(x)在x∈[-4,4]上恰有7个零点,则实数m的取值范围为( )
| A. | (-∞,-e-2) | B. | (-1-e-2,-e-2) | C. | (-1-e-2,0) | D. | (-1-e-2,-1-3e-4) |
13.己知等差数列{an}中,a2=2,a5=5.
(Ⅰ)若bn=2${\;}^{{a}_{n}}$,求数列{bn}的前n项的和Sn
(Ⅱ)若c1=a1,cn-cn-1=an,求数列{cn}的通项公式.
(Ⅰ)若bn=2${\;}^{{a}_{n}}$,求数列{bn}的前n项的和Sn
(Ⅱ)若c1=a1,cn-cn-1=an,求数列{cn}的通项公式.
7.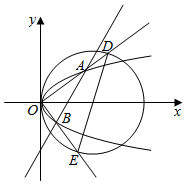 如图所示,过点(1,0)的直线与抛物线y2=x交于A、B两点,射线OA和OB分别和圆(x-2)2+y2=4交于D、E两点,若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ,则λ的最小值是( )
如图所示,过点(1,0)的直线与抛物线y2=x交于A、B两点,射线OA和OB分别和圆(x-2)2+y2=4交于D、E两点,若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ,则λ的最小值是( )
 如图所示,过点(1,0)的直线与抛物线y2=x交于A、B两点,射线OA和OB分别和圆(x-2)2+y2=4交于D、E两点,若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ,则λ的最小值是( )
如图所示,过点(1,0)的直线与抛物线y2=x交于A、B两点,射线OA和OB分别和圆(x-2)2+y2=4交于D、E两点,若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ,则λ的最小值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
11.不等式$\frac{2-x}{1+x}$≥0的解集为( )
| A. | (-1,2] | B. | [-1,2] | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-1]∪(2,+∞) |
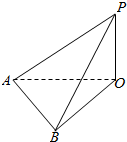 如图所示,在地面上有一旗杆OP,测得它的高度10m,在地面上取一基线AB,AB=20m,在A处测得P点的仰角∠OAP=30°,在B处测得P点的仰角∠OBP=45°,则∠AOB=$\frac{π}{2}$.
如图所示,在地面上有一旗杆OP,测得它的高度10m,在地面上取一基线AB,AB=20m,在A处测得P点的仰角∠OAP=30°,在B处测得P点的仰角∠OBP=45°,则∠AOB=$\frac{π}{2}$.