题目内容
20．直线2（m+1）x+（m-3）y-5m-1=0与圆（x-1）2+y2=3的位置关系是（ ）| A． | 相交 | B． | 相切 | C． | 相离 | D． | 无法判断 |
分析 确定直线过定点（2，1）在圆（x-1）2+y2=3内，即可得出结论．
解答 解：由2（m+1）x+（m-3）y-5m-1=0可得m（2x+y-5）+（2x-3y-1）=0
∴$\left\{\begin{array}{l}{2x+y-5=0}\\{2x-3y-1=0}\end{array}\right.$，∴$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$，
∵（2-1）2+12=2＜3，
∴（2，1）在圆（x-1）2+y2=3内，
∴直线2（m+1）x+（m-3）y-5m-1=0与圆（x-1）2+y2=3相交，
故选：A．
点评 本题考查直线过定点，考查直线与圆的位置关系，确定直线过定点是关键．
练习册系列答案
导学全程练创优训练系列答案
相关题目
11．不等式$\frac{2-x}{1+x}$≥0的解集为（ ）
| A． | （-1，2] | B． | [-1，2] | C． | （-∞，-1）∪（2，+∞） | D． | （-∞，-1]∪（2，+∞） |
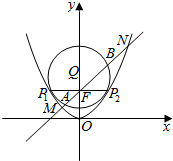如图，抛物线C：x2=2py（p＞0）的焦点为F（0，1），取垂直于y轴的直线与抛物线交于不同的两点P1，P2．过P1，P2作圆心为Q的圆，使抛物线的其余点均在圆外，且P1Q⊥P2Q．
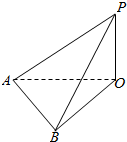如图所示，在地面上有一旗杆OP，测得它的高度10m，在地面上取一基线AB，AB=20m，在A处测得P点的仰角∠OAP=30°，在B处测得P点的仰角∠OBP=45°，则∠AOB=$\frac{π}{2}$．