题目内容
1.甲、乙两个粮库要项A,B量诊运送大米,已知甲库将调出100吨大米,乙库将调出80吨大米,A镇至少需要60吨大米,B镇至少需要100吨大米,且甲往B镇运送大米的吨数不少于乙往A镇运送大米的吨数的2倍,两库到两镇运费如表(其中a为常数,$\frac{1}{2}$<a<2).| 运费(元/吨) | ||
| 甲库 | 乙库 | |
| A镇 | 240+10a | 180 |
| B镇 | 260 | 210 |
分析 列出线性约束条件,目标函数,作出可行域,求出最值,可得结论.
解答 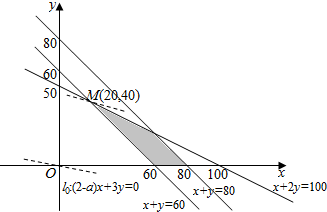 解:设甲、乙库往A镇运送x、y 吨大米,则甲、乙库往B镇运送100-x、80-y吨大米.
解:设甲、乙库往A镇运送x、y 吨大米,则甲、乙库往B镇运送100-x、80-y吨大米.
依题意有:$\left\{\begin{array}{l}{x+y≥60}\\{(100-x)+(80-y)≥100}\\{100-x≥2y}\\{x,y≥0}\end{array}\right.$,整理得:$\left\{\begin{array}{l}{60≤x+y≤80}\\{x+2y≤100}\\{x,y≥0}\end{array}\right.$,
根据上述约束条件作出可行域,如下图所示:
设总运费为z,则z=(240+10a)x+260(100-x)+180y+210(80-y)=(10a-20)x-30y+42800
目标直线为l:y=$\frac{a-2}{3}$x+$\frac{4280}{3}$-$\frac{z}{30}$,
且l越上移z的值越小,因为$\frac{1}{2}$<a<2,所以斜率$\frac{a-2}{3}$∈(-$\frac{1}{2}$,0),
如图,当l过点M(20,40)时,Z的值取得最小,
答:应该按甲库往A镇运送的大米量为20吨;乙库往A镇运送的大米量为40吨的方案派送大米,总运费最省.
点评 本题考查线性规划知识的运用,考查利用数学知识解决实际问题,属于中档题.

练习册系列答案
相关题目
11.“2<m<6”是“方程(6-m)x2+(m-2)y2=-m2+8m-12表示椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.已知f(x)是定义在R上的函数,且满足①f(4)=0;②曲线y=f(x+1)关于点(-1,0)对称;③x∈(-4,0)时,f(x)=log2($\frac{x}{{e}^{|x|}}$+ex-m).若y=f(x)在x∈[-4,4]上恰有7个零点,则实数m的取值范围为( )
| A. | (-∞,-e-2) | B. | (-1-e-2,-e-2) | C. | (-1-e-2,0) | D. | (-1-e-2,-1-3e-4) |
16.命题p“若sinα=$\frac{1}{2}$,则α=30°;命题q:若点(m,n)在直线x+y+1=0的上方,则m+n+1>0,下列命题是真命题的是( )
| A. | p∨¬q | B. | ¬p∧q | C. | ¬q∧¬q | D. | p∧q |
6.等比数列{an}中各项均为正数a1a5=4,a4=1,则{an}的公比q为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | ±$\frac{1}{2}$ | D. | ±2 |
13.己知等差数列{an}中,a2=2,a5=5.
(Ⅰ)若bn=2${\;}^{{a}_{n}}$,求数列{bn}的前n项的和Sn
(Ⅱ)若c1=a1,cn-cn-1=an,求数列{cn}的通项公式.
(Ⅰ)若bn=2${\;}^{{a}_{n}}$,求数列{bn}的前n项的和Sn
(Ⅱ)若c1=a1,cn-cn-1=an,求数列{cn}的通项公式.
11.不等式$\frac{2-x}{1+x}$≥0的解集为( )
| A. | (-1,2] | B. | [-1,2] | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-1]∪(2,+∞) |