题目内容
 如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=| 1 |
| 3 |
(Ⅰ)求证:AB⊥CE;
(Ⅱ)若AC=CE,求二面角A-CD-B的余弦值.
考点:与二面角有关的立体几何综合题,棱锥的结构特征
专题:空间位置关系与距离,空间角
分析:(Ⅰ)设DE=a,由已知条件利用余弦定理求出CD=
a,CE=a,从而得到∠BCE=90°,由此能证明EC⊥平面ABC,从而得到EC⊥AB.
(Ⅱ)取BC中点O,BE中点F,以O为原点建立如图所示的空间直角坐标系o-xyz,利用向量法能求出二面角A-CD-B的余弦值.
| 3 |
(Ⅱ)取BC中点O,BE中点F,以O为原点建立如图所示的空间直角坐标系o-xyz,利用向量法能求出二面角A-CD-B的余弦值.
解答:
(Ⅰ)证明:△DCB中,CB=CD,∠DCB=120°,
∴∠CDB=30°,设DE=a,∵DE=
DB.∴BD=3a,解得CD=
a,
在△CDE中,由余弦定理,得:CE=
=a,
∴∠DCE=30°,∴∠BCE=90°,∴EC⊥BC,
∵平面ABC⊥平面BCD,交线为BC,
∴EC⊥平面ABC,∴EC⊥AB.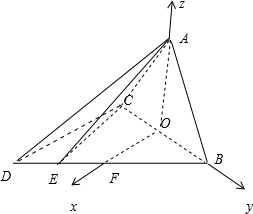
(Ⅱ)解:取BC中点O,BE中点F,连结OA,OF,
∵AC=AB,∴AO⊥BC,
∵平面ABC⊥平面BCD,交线为BC,
∴AO⊥平面BCD,
∵O是BC中点,F是BE中点,
∴OF∥EC,由(1)知,EC⊥BC,∴OF⊥BC,
以O为原点建立如图所示的空间直角坐标系o-xyz,
设DE=2,得A(0,0,1),B(0,
,0),
C(0,-
,0),D(3,-2
,0),
∴
=(0,-
,-1),
=(3,-
,0),
设平面ACD的法向量
=(1,
,-3),
又平面BCD的法向量
=(0,0,1),
∴cos<
,
>=
=-
,
∴二面角A-CD-B的余弦值为
.
∴∠CDB=30°,设DE=a,∵DE=
| 1 |
| 3 |
| 3 |
在△CDE中,由余弦定理,得:CE=
3a2+a2-2
|
∴∠DCE=30°,∴∠BCE=90°,∴EC⊥BC,
∵平面ABC⊥平面BCD,交线为BC,
∴EC⊥平面ABC,∴EC⊥AB.

(Ⅱ)解:取BC中点O,BE中点F,连结OA,OF,
∵AC=AB,∴AO⊥BC,
∵平面ABC⊥平面BCD,交线为BC,
∴AO⊥平面BCD,
∵O是BC中点,F是BE中点,
∴OF∥EC,由(1)知,EC⊥BC,∴OF⊥BC,
以O为原点建立如图所示的空间直角坐标系o-xyz,
设DE=2,得A(0,0,1),B(0,
| 3 |
C(0,-
| 3 |
| 3 |
∴
| AC |
| 3 |
| CD |
| 3 |
设平面ACD的法向量
| n1 |
| 3 |
又平面BCD的法向量
| n2 |
∴cos<
| n1 |
| n2 |
| -3 | ||
|
3
| ||
| 13 |
∴二面角A-CD-B的余弦值为
3
| ||
| 13 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
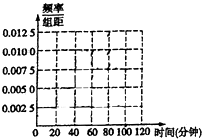 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示: 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.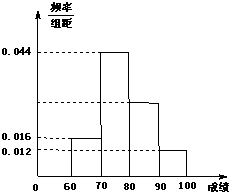 某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.
某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.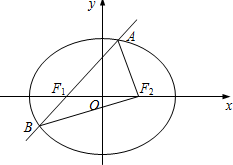 如图,椭圆E:
如图,椭圆E: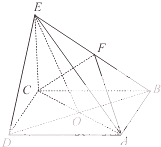 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.