题目内容
下列命题中正确的个数为( )
(1)命题“?x>0,x2-x≤0”的否定是“?x≤0,x2-x>0”
(2)函数y=sin(x-
)在[0,π]上为减函数
(3)已知数列{an},则“an,an+1,an+2成等比数列”是“an+12=anan+2”的充要条件
(4)已知函数f(x)=lgx+
,则函数f(x)的最小值为2.
(1)命题“?x>0,x2-x≤0”的否定是“?x≤0,x2-x>0”
(2)函数y=sin(x-
| π |
| 2 |
(3)已知数列{an},则“an,an+1,an+2成等比数列”是“an+12=anan+2”的充要条件
(4)已知函数f(x)=lgx+
| 1 |
| lgx |
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:综合题
分析:(1)中,写出命题p的否定¬p,判定命题(1)是否正确;
(2)中,由x∈[0,π]时,判定函数y=sin(x-
)在[0,π]上是增函数;
(3)中,可以举例说明充分与必要条件不成立;
(4)中,讨论函数f(x)的值域是什么,从而判定命题是否正确.
(2)中,由x∈[0,π]时,判定函数y=sin(x-
| π |
| 2 |
(3)中,可以举例说明充分与必要条件不成立;
(4)中,讨论函数f(x)的值域是什么,从而判定命题是否正确.
解答:
解:对于(1),命题“?x>0,x2-x≤0”的否定是“?x>0,x2-x>0”,
∴命题(1)正确;
对于(2),∵x∈[0,π],∴x-
∈[-
,
],
∴函数y=sin(x-
)在[0,π]上是增函数,
∴命题(2)错误;
对于(3),在数列{an}中,当an,an+1,an+2成等比数列时,an+12=anan+2,
反之,不成立,如a1=a2=…=an=0时,
∴命题(3)不正确;
对于(4),∵函数f(x)=lgx+
,∴x>0且x≠1,∴当x>1时,f(x)≥2,当1>x>0时,f(x)≤-2;
∴命题(4)错误.
所以,以上正确的命题有1个;
故选:A.
∴命题(1)正确;
对于(2),∵x∈[0,π],∴x-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴函数y=sin(x-
| π |
| 2 |
∴命题(2)错误;
对于(3),在数列{an}中,当an,an+1,an+2成等比数列时,an+12=anan+2,
反之,不成立,如a1=a2=…=an=0时,
∴命题(3)不正确;
对于(4),∵函数f(x)=lgx+
| 1 |
| lgx |
∴命题(4)错误.
所以,以上正确的命题有1个;
故选:A.
点评:本题通过命题真假的判定,考查了命题的否定、函数的单调性与最值问题以及充分与必要条件问题,是综合题,解题时应对每一个选项,仔细分析,选出正确的答案.

练习册系列答案
相关题目
读程序:
S=0
sum=0
for i=1 to 100
S=S+i
i=i+1
sum=sum+S
next
输出sum
该程序的运行结果是( )的值.
S=0
sum=0
for i=1 to 100
S=S+i
i=i+1
sum=sum+S
next
输出sum
该程序的运行结果是( )的值.
| A、1+2+3+…+99 |
| B、1+2+3+…+100 |
| C、1+(1+2)+(1+2+3)+…+(1+2+3+…+99) |
| D、1+(1+2)+(1+2+3)+…+(1+2+3+…+100) |
设x,y∈R,条件甲:
+
≤1,条件乙:
,则条件甲是条件乙的( )
| x2 |
| 25 |
| y2 |
| 9 |
|
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,设函数f(x)=g(2x-1),则曲线y=f(x)在点(1,f(1))处切线方程为( )
| A、y=2x+1 |
| B、y=4x-1 |
| C、y=2x-1 |
| D、y=4x+1 |
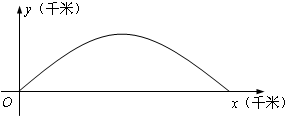 如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-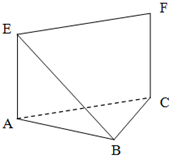 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.