题目内容
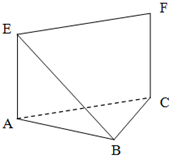 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.(Ⅰ)求证:AB⊥平面BCF;
(Ⅱ)求二面角A-EB-F的某三角函数值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间角
分析:(Ⅰ)由已知条件推导出AB⊥BC,AB⊥FC,由此能证明AB⊥平面BCF.
(Ⅱ)取BE的中点G,连接FG,由已知条件推导出∠AGF即为二面角A-EB-F的平面角.利用余弦定理能求出二面角A-EB-F的余弦值.
(Ⅱ)取BE的中点G,连接FG,由已知条件推导出∠AGF即为二面角A-EB-F的平面角.利用余弦定理能求出二面角A-EB-F的余弦值.
解答:
(Ⅰ)证明:∵∠ABC=90°,∴AB⊥BC,
又∵EA⊥平面ABC,FC∥EA,∴AB⊥FC,
∵BC∩FC=C,
∴AB⊥平面BCF.
(Ⅱ)解:取BE的中点G,连接FG,
∵EA=BA,∴AC⊥EB,
又∵EF=FB=
a,∴FG⊥EB,
∴∠AGF即为二面角A-EB-F的平面角.
在△AGF中,AF=
a,AG=
a,FG=
a
由余弦定理有cos∠AGF=
=
=-
∴二面角A-EB-F的余弦值是-
.
又∵EA⊥平面ABC,FC∥EA,∴AB⊥FC,
∵BC∩FC=C,
∴AB⊥平面BCF.
(Ⅱ)解:取BE的中点G,连接FG,

∵EA=BA,∴AC⊥EB,
又∵EF=FB=
| 2 |
∴∠AGF即为二面角A-EB-F的平面角.
在△AGF中,AF=
| 3 |
| ||
| 2 |
| ||
| 2 |
由余弦定理有cos∠AGF=
| AG2+FG2-AF2 |
| 2AG•FG |
| ||||||||
2•
|
| ||
| 3 |
∴二面角A-EB-F的余弦值是-
| ||
| 3 |
点评:本题考查直线与平面垂直的证明,考查二面角的某三角函数值的求法,解题时要认真审题,合理地化空间问题为平面问题,注意余弦定理的合理运用.

练习册系列答案
相关题目
若直线
+
=1(a>0,b>0)始终平分圆x2+y2-4x-2y-8=0的周长,则ab的取值范围是( )
| x |
| a |
| y |
| b |
A、(-∞,
| ||
B、(0,
| ||
| C、(0,8] | ||
| D、[8,+∞) |