题目内容
已知函数f(x)=
,其中a为常数,且函数f(x)是奇函数.
(1)求a的值;
(2)判断函数f(x)在区间(0,+∞)的单调性,并给予证明;
(3)求函数f(x)的值域.
| 2x-a |
| 2x+1 |
(1)求a的值;
(2)判断函数f(x)在区间(0,+∞)的单调性,并给予证明;
(3)求函数f(x)的值域.
考点:奇偶性与单调性的综合,函数的值域,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)通过奇函数的定义,比较系数,即可求a的值;
(2)直接判断函数f(x)在区间(0,+∞)的单调性,利用函数的单调性的定义证明;
(3)利用反函数的定义域,求解函数f(x)的值域.
(2)直接判断函数f(x)在区间(0,+∞)的单调性,利用函数的单调性的定义证明;
(3)利用反函数的定义域,求解函数f(x)的值域.
解答:
解:(1)函数f(x)是奇函数,所以对任意实数x(x≠0),
都有f(-x)=-f(x),即
=-
,
整理得(a+1)(2x-1)=0,
因为2x-1不恒为零,所以a+1=0,a=-1.…(4分)
(2)函数f(x)=
(0,+∞)是增函数,证明如下:
在区间(0,+∞)上任取x1>x2>0,则2x1-2x2>0,(2x1+1)(2x2+1)>0,
所以f(x1)-f(x2)=
-
=
>0,结论成立.…(10分)
(3)设y=
,整理得2x=
(y≠1),由2x>0,
>0,
解得-1<y<1,故函数的值域为(-1,1). …(16分)
都有f(-x)=-f(x),即
| 2-x-a |
| 2-x+1 |
| 2x-a |
| 2x+1 |
整理得(a+1)(2x-1)=0,
因为2x-1不恒为零,所以a+1=0,a=-1.…(4分)
(2)函数f(x)=
| 2x-1 |
| 2x+1 |
在区间(0,+∞)上任取x1>x2>0,则2x1-2x2>0,(2x1+1)(2x2+1)>0,
所以f(x1)-f(x2)=
| 2x1-1 |
| 2x1+1 |
| 2x2-1 |
| 2x2+1 |
| 2(2x1-2x2) |
| (2x1+1)(2x2+1) |
(3)设y=
| 2x-1 |
| 2x+1 |
| y+1 |
| 1-y |
| y+1 |
| 1-y |
解得-1<y<1,故函数的值域为(-1,1). …(16分)
点评:本题考查函数的奇偶性与单调性的应用,反函数的应用,考查分析问题解决问题的能力.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
已知函数f[lg(x+1)]的定义域是(0、9],则f(x2)的定义域是( )
| A、[-1,1] |
| B、(-1,1) |
| C、[-1,0)∪(0,1] |
| D、(-1,0)∪(0,1) |
设A(-2,0),B(2,0),条件甲:“△ABC是以C为直角顶点的三角形”;条件乙:“C的坐标是方程x2+y2=4的解”,那么甲是乙的( )
| A、必要非充分条件 |
| B、充要条件 |
| C、充分非必要条件 |
| D、既不充分也非必要条件 |
方程lnx+2x=6的根属于区间( )
| A、(1,2) | ||||
B、(
| ||||
C、(1,
| ||||
D、(
|
函数y=
的图象大致为( )
| cos3x |
| 3x-3-x |
A、 |
B、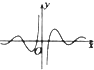 |
C、 |
D、 |