题目内容
把一个周长为18cm的长方形围成一个圆柱.
(1)求圆柱的体积V(x)关于圆柱底面周长x的函数,并指出定义域;
(2)当圆柱的体积V(x)最大时,求圆柱的底面周长与高的比值.
(1)求圆柱的体积V(x)关于圆柱底面周长x的函数,并指出定义域;
(2)当圆柱的体积V(x)最大时,求圆柱的底面周长与高的比值.
考点:基本不等式
专题:导数的综合应用
分析:(1)根据圆的周长表示出半径,再根据圆柱的体积公式,求出体积即可,根据函数的实际意义求出定义域,
(2)利用导数求出圆柱的体积的最大值时x的值,即可求出圆柱的底面周长与高的比值.
(2)利用导数求出圆柱的体积的最大值时x的值,即可求出圆柱的底面周长与高的比值.
解答:
解:(1)因为圆柱底面周长x为长方形一条边长,
所以圆柱的高是另一边长为(
-x)=(9-x),
因为设圆柱的底面半径为r,
则2πr=x,
解得r=
,
所以V(x)=π(
)2•(9-x)=
(9x2-x3),定义域为(0,9),
(2)V′(x)=
(18x-3x2),
令V′(x)=0,解得x=6,
当V′(x)>0,即0<x<6时,函数递增,
当V′(x)<0,即6<x<9时,函数递减,
故当x=6时,函数V(x)有最大值,
此时圆柱的高为9-6=3,
故圆柱的底面周长与高的比值为
=2.
所以圆柱的高是另一边长为(
| 18 |
| 2 |
因为设圆柱的底面半径为r,
则2πr=x,
解得r=
| x |
| 2π |
所以V(x)=π(
| x |
| 2π |
| 1 |
| 4π |
(2)V′(x)=
| 1 |
| 4π |
令V′(x)=0,解得x=6,
当V′(x)>0,即0<x<6时,函数递增,
当V′(x)<0,即6<x<9时,函数递减,
故当x=6时,函数V(x)有最大值,
此时圆柱的高为9-6=3,
故圆柱的底面周长与高的比值为
| 6 |
| 3 |
点评:本题考查了导数的再几何中的应用,关键是利用导数求出函数最值,属于中档题

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
执行右面的程序框图,输出的S是( )


| A、18 | B、28 | C、40 | D、56 |
若“对任意的实数x,不等式x2+2x+a>0均成立”是假命题,则实数a的取值范围( )
| A、(1,+∞) |
| B、[1,+∞) |
| C、(-∞,1) |
| D、(-∞,1] |
下列函数中,既是奇函数又是减函数的是( )
A、y=
| ||
| B、y=-tanx | ||
C、y=
| ||
| D、y=-x3(-1<x≤1) |
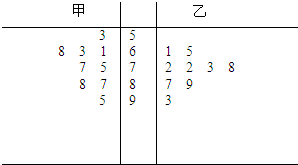 某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图
某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图