题目内容
函数y=lg(-x2+2x+8)的单调递减区间为 .
考点:对数函数的图像与性质
专题:计算题,函数的性质及应用
分析:由复合函数的单调性知,y=-x2+2x+8单调递减且y>0;从而解得.
解答:
解:由复合函数的单调性知,
y=-x2+2x+8单调递减且y>0;
即
,
解得,x∈(1,4),
故函数y=lg(-x2+2x+8)的单调递减区间为(1,4);
故答案为:(1,4).
y=-x2+2x+8单调递减且y>0;
即
|
解得,x∈(1,4),
故函数y=lg(-x2+2x+8)的单调递减区间为(1,4);
故答案为:(1,4).
点评:本题考查了对数函数与二次函数的单调性及复合函数单调性的应用,属于基础题.

练习册系列答案
相关题目
若“对任意的实数x,不等式x2+2x+a>0均成立”是假命题,则实数a的取值范围( )
| A、(1,+∞) |
| B、[1,+∞) |
| C、(-∞,1) |
| D、(-∞,1] |
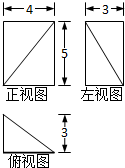
已知某几何体的三视图如图所示,则该几何体的体积等于( )


A、
| ||
| B、32 | ||
C、
| ||
D、
|
下列函数中,既是奇函数又是减函数的是( )
A、y=
| ||
| B、y=-tanx | ||
C、y=
| ||
| D、y=-x3(-1<x≤1) |
设集合A={x|y=lg(x-3)},B={x|x2-5x+5<0},则A∩B=( )
| A、∅ | ||||
B、(3,
| ||||
| C、(-2,1) | ||||
| D、(4,+∞) |