Question

设A（-2，0），B（2，0），条件甲：“△ABC是以C为直角顶点的三角形”；条件乙：“C的坐标是方程x²+y²=4的解”，那么甲是乙的（　　）

• A、必要非充分条件
• B、充要条件
• C、充分非必要条件
• D、既不充分也非必要条件

Answer 1

考点：必要条件、充分条件与充要条件的判断

专题：简易逻辑

分析：可结合图形，当△ABC是以C为直角顶点的三角形时，该点C在圆x²+y²=4上，即得到条件乙；而条件乙得不出条件甲，因为C点和A或B重合时，三点A，B，C构不成三角形，所以最后可得到甲是乙的充分非必要条件．

解答： 解：如图，

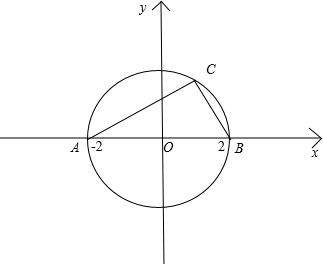
（1）若条件甲成立，则C点必然在以O为圆心，半径为2的圆上；
∴该点坐标满足圆的方程x²+y²=4，即C的坐标是该方程的解，所以得到条件乙成立；
∴甲是乙的充分条件；
（2）若条件乙成立，则C点在以O为圆心，半径为2的圆上；
当C和A，或B重合时，A，B，C三点不构成三角形；
即条件乙得不到条件甲；
∴甲不是乙的必要条件；
∴甲是乙的充分不必要条件．
故选C．

点评：考查圆的性质：圆上任意一点和不过该点的直径两端点连线相互垂直，曲线上的点的坐标和曲线方程的关系，以及充分条件、必要条件、充分不必要条件的概念．