题目内容
函数y=
的图象大致为( )
| cos3x |
| 3x-3-x |
A、 |
B、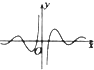 |
C、 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:现根据函数的奇偶性排除A,再根据函数值y的情况排除B,再利用极限的思想排除C,问题得以解决
解答:
解:∵f(-x)=
=-
=f(x),
∴函数f(x)为奇函数,故排除A,
当x>0时,3x>3-x,当x<0时,3x<3-x,
当2kπ<3x<2kπ+
,即
<x<
+
时,cos3x>0,故y>0,故排除B,
因为
=0,
故排除C,
故选:D
| cos(-3x) |
| 3-x-3x |
| cos3x |
| 3x-3-x |
∴函数f(x)为奇函数,故排除A,
当x>0时,3x>3-x,当x<0时,3x<3-x,
当2kπ<3x<2kπ+
| π |
| 2 |
| 2kπ |
| 3 |
| 2kπ |
| 3 |
| π |
| 6 |
因为
| lim |
| n→∞ |
| cos3x |
| 3x-3-x |
故排除C,
故选:D
点评:本题考查了函数的图象的识别,函数的奇偶性,函数值,极限是常用的方法,属于中档题

练习册系列答案
相关题目
执行右面的程序框图,输出的S是( )


| A、18 | B、28 | C、40 | D、56 |
若“对任意的实数x,不等式x2+2x+a>0均成立”是假命题,则实数a的取值范围( )
| A、(1,+∞) |
| B、[1,+∞) |
| C、(-∞,1) |
| D、(-∞,1] |
已知an=2,amn=16,则m的值为( )
| A、3 |
| B、4 |
| C、a3 |
| D、a6 |