题目内容
4．设函数f（x）=$\frac{ln（{x}^{2}+3x-4）}{x-2}$，求f（x）的定义域．分析 直接由对数的真数大于0且分式的分母不等于0，求解即可得答案．
解答 解：由$\left\{\begin{array}{l}{{x}^{2}+3x-4＞0}\\{x-2≠0}\end{array}\right.$，解得x＜-4或x＞1且x≠2，
∴函数f（x）=$\frac{ln（{x}^{2}+3x-4）}{x-2}$的定义域是{x|x＜-4或x＞1且x≠2}．
点评 本题考查了函数的定义域及其求法，考查了对数函数的性质，是基础题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
在四棱锥P-ABCD中，已知DC∥AB，DC=2AB，E为棱PD的中点．
15．
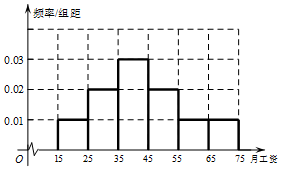为了解某单位员工的月工资水平，从该单位500位员工中随机抽取了50位进行调查，得到如下频数分布表和频率分布直方图：
（1）试由图估计该单位员工月平均工资；
（2）现用分层抽样的方法从月工资在[45，55）和[55，65）的两组所调查的男员工中随机选取5人，问各应抽取多少人？
（3）若从月工资在[25，35）和[45，55）两组所调查的女员工中随机选取2人，试求这2人月工资差不超过1000元的概率．
为了解某单位员工的月工资水平，从该单位500位员工中随机抽取了50位进行调查，得到如下频数分布表和频率分布直方图：| 月工资 （单位：百元） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75） |
| 男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
| 女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
（2）现用分层抽样的方法从月工资在[45，55）和[55，65）的两组所调查的男员工中随机选取5人，问各应抽取多少人？
（3）若从月工资在[25，35）和[45，55）两组所调查的女员工中随机选取2人，试求这2人月工资差不超过1000元的概率．
12．已知{an}是等比数列，那么下列结论错误的是（ ）
| A． | ${a_5}^2={a_3}•{a_7}$ | B． | ${a_5}^2={a_1}•{a_9}$ | ||
| C． | ${a_n}^2={a_{n-1}}•{a_{n+1}}（{n∈{N^*}}）$ | D． | ${a_n}^2={a_{n-k}}•{a_{n+k}}（{k∈{N^*}，n＞k＞0}）$ |
19．国内某汽车品牌一个月内被消费者投诉的次数用X表示，据统计，随机变量X的概率分布如下：
（1）求a的值；
（2）假设一月份与二月份被消费者投诉的次数互不影响，求该汽车品牌在这两个月内共被消费者投诉2次的概率．
| X | 0 | 1 | 2 | 3 |
| P | 0.1 | 0.3 | 2a | a |
（2）假设一月份与二月份被消费者投诉的次数互不影响，求该汽车品牌在这两个月内共被消费者投诉2次的概率．
9．设函数f（x）（x∈R）为奇函数，f（1）=$\frac{1}{2}$，f（x+2）=f（x）+f（2），则f（-5）=（ ）
| A． | -$\frac{5}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{5}{2}$ | D． | 5 |
