题目内容
14. 在四棱锥P-ABCD中,已知DC∥AB,DC=2AB,E为棱PD的中点.
在四棱锥P-ABCD中,已知DC∥AB,DC=2AB,E为棱PD的中点.(1)求证:AE∥平面PBC;
(2)若PB⊥PC,PB⊥AB,求证:平面PAB⊥平面PCD.
分析 (1)取PC中点E,连结EF、BF,推导出四边形ABFE是平行四边形,从而AE∥BF,由此能证明AE∥平面PBC.
(2)由DC∥AB,PB⊥PC,PB⊥AB,得PB⊥CD,从而PB⊥平面PCD,由此能证明平面PAB⊥平面PCD.
解答 证明:(1) 取PC中点E,连结EF、BF,
取PC中点E,连结EF、BF,
∵在四棱锥P-ABCD中,DC∥AB,DC=2AB,E为棱PD的中点,
∴EF$\underset{∥}{=}$$\frac{1}{2}$CD,AB$\underset{∥}{=}$$\frac{1}{2}CD$,
∴EF$\underset{∥}{=}$AB,∴四边形ABFE是平行四边形,∴AE∥BF,
∵AE?平面PBC,BF?平面PBC,
∴AE∥平面PBC.
(2)∵DC∥AB,PB⊥PC,PB⊥AB,
∴PB⊥CD,
∵PC∩CD=C,∴PB⊥平面PCD,
∵PB?平面PAB,∴平面PAB⊥平面PCD.
点评 本题考查线面平行、面面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.

练习册系列答案
相关题目
16.抛物线$y=\frac{1}{4}{x^2}$的焦点坐标为( )
| A. | (-1,0) | B. | (1,0) | C. | (0,-1) | D. | (0,1) |
6.为调查大学生这个微信用户群体中每人拥有微信群的数量,现从武汉市大学生中随机抽取100位同学进行了抽样调查,结果如下:
(Ⅰ)求a,b,c的值;
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.
| 微信群数量 | 频数 | 频率 |
| 0至5个 | 0 | 0 |
| 6至10个 | 30 | 0.3 |
| 11至15个 | 30 | 0.3 |
| 16至20个 | a | c |
| 20个以上 | 5 | b |
| 合计 | 100 | 1 |
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.
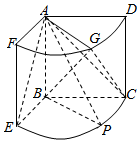 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点. 如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=$\frac{1}{2}$EA=1.则直线EB与平面ECF所成角的正弦值为$\frac{\sqrt{3}}{6}$.
如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=$\frac{1}{2}$EA=1.则直线EB与平面ECF所成角的正弦值为$\frac{\sqrt{3}}{6}$.