题目内容
19.国内某汽车品牌一个月内被消费者投诉的次数用X表示,据统计,随机变量X的概率分布如下:| X | 0 | 1 | 2 | 3 |
| P | 0.1 | 0.3 | 2a | a |
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该汽车品牌在这两个月内共被消费者投诉2次的概率.
分析 (1)由随机变量X的概率分布列的性质能求出a.
(2)由随机变量X的概率分布列,得该汽车品牌在这两个月内共被消费者投诉2次的概率p=P(X=0)P(X=2)+P(X=2)P(X=0)+P(X=1)P(X=1),由此能求出结果.
解答 解:(1)由随机变量X的概率分布列的性质得:
0.1+0.3+2a+a=1,
解得a=0.2.
(2)由随机变量X的概率分布列,得:
该汽车品牌在这两个月内共被消费者投诉2次的概率:
p=P(X=0)P(X=2)+P(X=2)P(X=0)+P(X=1)P(X=1)
=0.1×0.4+0.4×0.1+0.3×0.3
=0.17.
点评 本题考查概率的求法及应用,是基础题,解题时要认真审题,注意随机变量的概率分布列的性质的合理运用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
11.定义域为R的可导函数y=f(x)的导函数为f′(x),满足f(x)>f′(x),且f(0)=3,则不等式f(x)<3ex的解集为( )
| A. | (-∞,0) | B. | (-∞,2) | C. | (0,+∞) | D. | (2,+∞) |
12.一动圆与定圆F:(x+2)2+y2=1相外切,且与直线l:x=1相切,则动圆圆心轨迹方程为( )
| A. | y2=4x | B. | y2=2x | C. | y2=-4x | D. | y2=-8x |
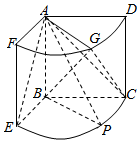 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点. 已知$\overrightarrow{a}$=2(cosωx,cosωx),$\overrightarrow{b}$=(cosωx,$\sqrt{3}$sinωx)(其中0<ω<1),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,
已知$\overrightarrow{a}$=2(cosωx,cosωx),$\overrightarrow{b}$=(cosωx,$\sqrt{3}$sinωx)(其中0<ω<1),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,