题目内容
15.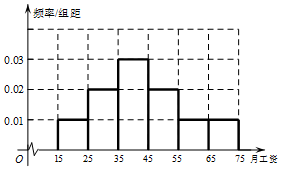 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:| 月工资 (单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
| 女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
分析 (1)由频率分布直方图能估计该单位员工月平均工资.
(2)用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,能求出月工资在[45,55)中抽取的人数和月工资在[55,65)中抽取的人数.
(3)由上表可知:月工资在[25,35)组的有两名女工,分别记作甲和乙,月工资在[45,55)组的有四名女工,分别记作A,B,C,D.现在从这6人中随机选取2人利用列举法求出基本事件有15组,其中月工资差不超过1000元,即为同一组的有7组,由此能求出这2人月工资差不超过1000元的概率.
解答 (本题满分12分)
(1)由频率分布直方图估计该单位员工月平均工资为:
20×0.01×10+30×0.02×10+40×0.03×10++50×0.02×10+60×0.01×10+70×0.01×10=43(百元),
即该单位员工月平均工资估计为4300元.…(4分)
(2)用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,
则月工资在[45,55)中抽取:5×$\frac{6}{6+4}$=3人,
月工资在[55,65)中抽取:5×$\frac{4}{6+4}$=2人. …(6分)
(3)由上表可知:月工资在[25,35)组的有两名女工,分别记作甲和乙,
月工资在[45,55)组的有四名女工,分别记作A,B,C,D.现在从这6人中随机选取2人的基本事件有如下15组:
(甲,乙),(甲,A),(甲,B),(甲,C),(甲,D),
(乙,A),(乙,B),(乙,C),(乙,D),
(A,B),(A,C),(A,D),
(B,C),(B,D),
(C,D)
其中月工资差不超过1000元,即为同一组的有:
(甲,乙),(A,B),(A,C),(A,D),(B,C),(B,D),(C,D)共7组,
∴这2人月工资差不超过1000元的概率为p=$\frac{7}{15}$.…(12分)
点评 本题考查概率的求法,考查频率分布直方图、古典概型、列举法等基础知识,考查运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想,是基础题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 微信群数量 | 频数 | 频率 |
| 0至5个 | 0 | 0 |
| 6至10个 | 30 | 0.3 |
| 11至15个 | 30 | 0.3 |
| 16至20个 | a | c |
| 20个以上 | 5 | b |
| 合计 | 100 | 1 |
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.
| A. | ?x0∈R,${x_0}^2-{x_0}+1≤0$ | B. | ?x0∈R,${x_0}^2-{x_0}+1>0$ | ||
| C. | ?x∈R,x2-x+1≤0 | D. | ?x∈R,x2-x+1>0 |
 已知$\overrightarrow{a}$=2(cosωx,cosωx),$\overrightarrow{b}$=(cosωx,$\sqrt{3}$sinωx)(其中0<ω<1),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,
已知$\overrightarrow{a}$=2(cosωx,cosωx),$\overrightarrow{b}$=(cosωx,$\sqrt{3}$sinωx)(其中0<ω<1),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,