题目内容
16．下面是被严重破坏的频率分布表和频率分布直方图，根据残表和残图，则 p=30，q=0.1．| 分数段 | 频数 | |
| [60，70） | p | |
| [70，80） | 90 | |
| [80，90） | 60 | |
| [90，100] | 20 | q |
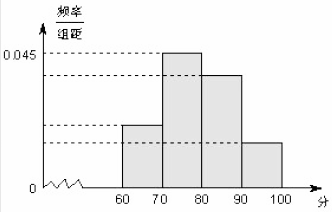
分析 由频率分布表得到[70，80）内的频数为90，由频率分布直方图得到[70，80）内的频率为0.45，从而出样本单元数n=200．由此能求出p，q．
解答 解：由频率分布表得到[70，80）内的频数为90，
由频率分布直方图得到[70，80）内的频率为0.45，
∴样本单元数n=$\frac{90}{0.45}$=200．
∴p=200-90-60-20=30．
q=$\frac{20}{200}$=0.1．
故答案为：30，0.1．
点评 本题考查频率分布表中的频数和频率的求法，是基础题，解题时要认真审题，注意频率分布表和频率分布直方图的性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．为调查大学生这个微信用户群体中每人拥有微信群的数量，现从武汉市大学生中随机抽取100位同学进行了抽样调查，结果如下：
（Ⅰ）求a，b，c的值；
（Ⅱ）以这100个人的样本数据估计武汉市的总体数据且以频率估计概率，若从全市大学生（数量很大）中随机抽取3人，记X表示抽到的是微信群个数超过15个的人数，求X的分布列和数学期望．
| 微信群数量 | 频数 | 频率 |
| 0至5个 | 0 | 0 |
| 6至10个 | 30 | 0.3 |
| 11至15个 | 30 | 0.3 |
| 16至20个 | a | c |
| 20个以上 | 5 | b |
| 合计 | 100 | 1 |
（Ⅱ）以这100个人的样本数据估计武汉市的总体数据且以频率估计概率，若从全市大学生（数量很大）中随机抽取3人，记X表示抽到的是微信群个数超过15个的人数，求X的分布列和数学期望．
已知$\overrightarrow{a}$=2（cosωx，cosωx），$\overrightarrow{b}$=（cosωx，$\sqrt{3}$sinωx）（其中0＜ω＜1），函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$，
11．定义域为R的可导函数y=f（x）的导函数为f′（x），满足f（x）＞f′（x），且f（0）=3，则不等式f（x）＜3ex的解集为（ ）
| A． | （-∞，0） | B． | （-∞，2） | C． | （0，+∞） | D． | （2，+∞） |
4．已知函数f（x）满足当x∈（1，2）时，f（x-1）=2f（$\frac{1}{x-1}$），当x∈（1，3]时，f（x）=lnx，若函数g（x）=$\frac{f（x）-ax}{x-1}$在区间[$\frac{1}{3}$，1）∪（1，3]上有三个不同的零点，则实数a的取值范围为（ ）
| A． | （0，$\frac{1}{，e}$） | B． | [$\frac{ln3}{3}$，$\frac{1}{，e}$） | C． | （$\frac{ln3}{3}$，$\frac{1}{，e}$） | D． | （0，$\frac{ln3}{3}$） |