题目内容
复数
在复平面上对应的点的坐标是（ ）
| (1+i)2 |
| 1-i |
| A、（1，1） |
| B、（-1，1） |
| C、（-1，-1） |
| D、（1，-1） |
考点：复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题：计算题,数系的扩充和复数
分析：先化简，由复数几何意义可求．
解答：
解：
=
=
=-1+i，
该复数对应的点为（-1，1），
故选B．
| (1+i)2 |
| 1-i |
| 2i |
| 1-i |
| 2i(1+i) |
| (1-i)(1+i) |
该复数对应的点为（-1，1），
故选B．
点评：该题考查复数代数形式的乘除运算、复数的几何意义，属基础题．
练习册系列答案
相关题目
如图，圆O与△ABC的边AB，AC分别相切于点B，D，与BC边相交于点E，且∠BED=60°，AB=1，则圆O的半径长为函数y=sin2x的一个单调区间是（ ）
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[
|
已知函数y=-x3+3x-a在[0，2]上有两个零点，则常数a的取值范围为（ ）
| A、0≤a＜2 |
| B、-2≤a≤2 |
| C、-2＜a＜2 |
| D、0≤a≤2 |
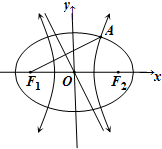如图，F1，F2是椭圆C1：| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 | ||
|
| 1 | ||
|
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
对实数m、n，定义运算“*”：m*n=
，设函数f（x）=（x2-3）*（x-2），x∈R．若函数y=f（x）+c的图象与x轴恰有两个公共点，则实数c的取值范围是（ ）
|
| A、（-3，1） |
| B、（-3，1] |
| C、（-3，-2]∪（0，1] |
| D、[2，3）∪[-1，0） |
由0，1，2，3这四个数字可以组成没有重复数字且不能被5整除的四位数的个数是（ ）
| A、24个 | B、12个 |
| C、6个 | D、4个 |
已知在△ABC中，角A，B，C的对边分别为a，b，c，已知点D是边BC的中点，且2
•
=a2-ac，则B的大小为（ ）
| AD |
| BC |
| A、45° | B、60° |
| C、90° | D、120° |