题目内容
已知函数y=-x3+3x-a在[0,2]上有两个零点,则常数a的取值范围为( )
| A、0≤a<2 |
| B、-2≤a≤2 |
| C、-2<a<2 |
| D、0≤a≤2 |
考点:函数零点的判定定理
专题:导数的综合应用
分析:通过对a分类讨论,利用导数研究函数的单调性极值与最值即可得出.
解答:
解:令f(x)=-x3+3x-a,x∈[0,2].
则f′(x)=-3x2+3=-3(x+1)(x-1),
令f′(x)=0,解得x=1.
列表如下:
由表格可知:当x=1时,函数f(x)取得极大值即最大值,f(1)=2-a;又f(0)=-a,f(2)=-2-a.∴最小值为-2-a.
①当a<0时,f(1)>0,f(0)>0,f(2)≥-2,因此函数f(x)最多有一个零点;
②当a≥2时,f(1)<0,因此函数f(x)无零点;
③当0≤a<2时,f(1)>0,f(0)≤0,f(2)<0,因此函数f(x)有两个零点,满足条件.
综上可得:只有当0≤a<2时,函数f(x)有两个零点.
故选:A.
则f′(x)=-3x2+3=-3(x+1)(x-1),
令f′(x)=0,解得x=1.
列表如下:
| x | [0,1) | 1 | (1,2] |
| f′(x) | + | 0 | - |
| f(x) | 单调递增 | 极大值 | 单调递减 |
①当a<0时,f(1)>0,f(0)>0,f(2)≥-2,因此函数f(x)最多有一个零点;
②当a≥2时,f(1)<0,因此函数f(x)无零点;
③当0≤a<2时,f(1)>0,f(0)≤0,f(2)<0,因此函数f(x)有两个零点,满足条件.
综上可得:只有当0≤a<2时,函数f(x)有两个零点.
故选:A.
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
圆(x-2)2+(y-1)2=4被双曲线
-
=1的一条渐近线截得的弦长为( )
| x2 |
| 9 |
| y2 |
| 16 |
A、2
| ||
| B、2 | ||
C、
| ||
| D、1 |
log26-log23=( )
| A、-2 | ||
| B、1 | ||
C、
| ||
| D、2 |
抛物线y2=-8x中,以(-1,1)为中点的弦所在的直线方程是( )
| A、x-4y-3=0 |
| B、x+4y+3=0 |
| C、4x+y-3=0 |
| D、4x+y+3=0 |
函数f(x)=sin(2x+
)(x∈R)的最小正周期为( )
| π |
| 3 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
复数
在复平面上对应的点的坐标是( )
| (1+i)2 |
| 1-i |
| A、(1,1) |
| B、(-1,1) |
| C、(-1,-1) |
| D、(1,-1) |
对命题“?x∈R,x≤0”的否定正确的是( )
| A、?x∈R,x>0 |
| B、?x∈R,x≤0 |
| C、?x∈R,x>0 |
| D、?x∈R,x≥0 |
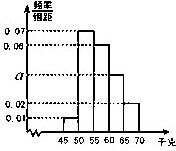 为了了解学生的身体状况,某校随机抽取了一批学生测量体重,经统计,这批学生的体重数据(单位为千克)全部介于45至70之间,将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70),得到如图所示的频率分布直方图,则a=
为了了解学生的身体状况,某校随机抽取了一批学生测量体重,经统计,这批学生的体重数据(单位为千克)全部介于45至70之间,将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70),得到如图所示的频率分布直方图,则a=