题目内容
对实数m、n,定义运算“*”:m*n=
,设函数f(x)=(x2-3)*(x-2),x∈R.若函数y=f(x)+c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
|
| A、(-3,1) |
| B、(-3,1] |
| C、(-3,-2]∪(0,1] |
| D、[2,3)∪[-1,0) |
考点:函数零点的判定定理,分段函数的应用
专题:函数的性质及应用
分析:由(x2-3)-(x-2)≤1,解得-1≤x≤2;由(x2-3)-(x-2)>1,解得x>2或x<-1.可得f(x)=
.分别画出函数y=f(x)与y=-c的图象,由图象即可以得到.
|
解答:
解:由(x2-3)-(x-2)≤1,化为x2-x-2≤0,解得-1≤x≤2;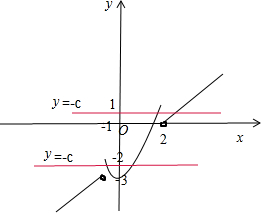
由(x2-3)-(x-2)>1,解得x>2或x<-1.
∴f(x)=
.
画出函数y=f(x)与y=-c的图象,
由图象可以得到:当且仅当-3<-c≤-2或0<-c≤1,即2≤c≤3或-1≤c<0时,两个函数y=f(x),y=-c的图象由两个交点,即函数y=f(x)+c的图象与x轴恰有两个公共点.
故选:D.

由(x2-3)-(x-2)>1,解得x>2或x<-1.
∴f(x)=
|
画出函数y=f(x)与y=-c的图象,
由图象可以得到:当且仅当-3<-c≤-2或0<-c≤1,即2≤c≤3或-1≤c<0时,两个函数y=f(x),y=-c的图象由两个交点,即函数y=f(x)+c的图象与x轴恰有两个公共点.
故选:D.
点评:本题考查了新定义、通过画出函数的图象的交点求出函数零点的个数,考查了数形结合的思想方法,属于中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
log26-log23=( )
| A、-2 | ||
| B、1 | ||
C、
| ||
| D、2 |
函数f(x)=sin(2x+
)(x∈R)的最小正周期为( )
| π |
| 3 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
复数
在复平面上对应的点的坐标是( )
| (1+i)2 |
| 1-i |
| A、(1,1) |
| B、(-1,1) |
| C、(-1,-1) |
| D、(1,-1) |
已知向量
=(1,0),
=(0,-1),
=k2
+k
(k≠0),
=
+
,如果
∥
,那么( )
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
A、k=1且
| ||||
B、k=1且
| ||||
C、k=-1且
| ||||
D、k=-1且
|
对命题“?x∈R,x≤0”的否定正确的是( )
| A、?x∈R,x>0 |
| B、?x∈R,x≤0 |
| C、?x∈R,x>0 |
| D、?x∈R,x≥0 |
已知sinθ=
,且cosθ<0,则tanθ等于( )
| 3 |
| 5 |
A、-
| ||
B、
| ||
| C、-3 | ||
| D、3 |