题目内容
如图，圆O与△ABC的边AB，AC分别相切于点B，D，与BC边相交于点E，且∠BED=60°，AB=1，则圆O的半径长为考点：与圆有关的比例线段
专题：选作题,立体几何
分析：求出∠BOD=120°，∠A=60°，利用AB=1，即可求出圆O的半径长．
解答：
解：如图所示，∵∠BED=60°，
∴∠F=60°，
∴∠BOD=120°，
∵圆O与△ABC的边AB，AC分别相切于点B，D，
∴OB⊥AB，OD⊥AD，
∴∠A=60°，
∵AB=1，
∴BD=1，
∴BF=
，
∴圆O的半径长为OB=
．
故答案为：
．
解：如图所示，∵∠BED=60°，∴∠F=60°，
∴∠BOD=120°，
∵圆O与△ABC的边AB，AC分别相切于点B，D，
∴OB⊥AB，OD⊥AD，
∴∠A=60°，
∵AB=1，
∴BD=1，
∴BF=
2
| ||
| 3 |
∴圆O的半径长为OB=
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查圆周角定理，考查学生的计算能力，确定∠BOD=120°，∠A=60°是关键．
练习册系列答案
名校课堂系列答案
相关题目
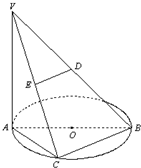如图，AB是圆O的直径，点C是弧AB的中点，D，E分别是VB，VC的中点，VA⊥平面ABC．
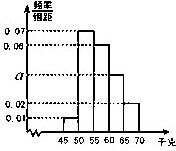为了了解学生的身体状况，某校随机抽取了一批学生测量体重，经统计，这批学生的体重数据（单位为千克）全部介于45至70之间，将数据分成以下5组：第1组[45，50），第2组[50，55），第3组[55，60），第4组[60，65），第5组[65，70），得到如图所示的频率分布直方图，则a=圆（x-2）2+（y-1）2=4被双曲线
-
=1的一条渐近线截得的弦长为（ ）
| x2 |
| 9 |
| y2 |
| 16 |
A、2
| ||
| B、2 | ||
C、
| ||
| D、1 |
复数
在复平面上对应的点的坐标是（ ）
| (1+i)2 |
| 1-i |
| A、（1，1） |
| B、（-1，1） |
| C、（-1，-1） |
| D、（1，-1） |