题目内容
已知函数f(x)=x+
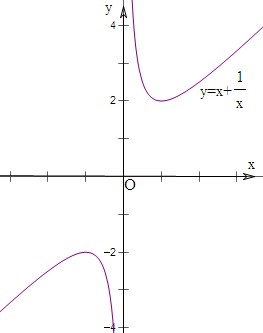
的定义域为(-∞,0)∪(0,+∞),求f(x)在(-∞,1)上的单调性并画出函数的图象.
| 1 |
| x |
考点:函数单调性的判断与证明,函数的图象
专题:作图题,函数的性质及应用
分析:根据函数单调性的定义求出函数f(x)在(-∞,1)上的单调区间,并注意讨论;判断函数的奇偶性,由对称画出函数f(x)的图象.
解答:
解:设x1<x2<1,
则f(x1)-f(x2)=(x1+
)-(x2+
)
=(x1-x2)(1-
)
∵x1<x2,∴x1-x2<0,
①当0<x1<x2<1时,0<x1x2<1,1-
<0,
∴f(x1)-f(x2)>0即f(x1)>f(x2),
∴f(x)在区间(0,1)上是减函数;
②当-1<x1<x2<0时,0<x1x2<1,1-
<0,
∴f(x1)-f(x2)>0即f(x1)>f(x2),
∴f(x)在区间(-1,0)上是减函数;
③当x1<x2<-1时,x1x2>1,1-
>0,
∴f(x1)-f(x2)<0即f(x1)<f(x2),
∴f(x)在区间(0,1)上是增函数.
∴函数f(x)在区间(-∞,1)上的单调性是:在(-∞,-1)上是增函数;
在(-1,0)和(0,1)上都是减函数;
∵f(x)=x+
的定义域为{x|x≠0},
f(-x)=-x+
=-f(x),
∴f(x)为奇函数,图象关于原点对称,
且函数f(x)在(-∞,-1),(1,+∞)上递增,在(-1,0),(0,1)上递减
故图象如图所示:
则f(x1)-f(x2)=(x1+
| 1 |
| x1 |
| 1 |
| x2 |
=(x1-x2)(1-
| 1 |
| x1x2 |
∵x1<x2,∴x1-x2<0,
①当0<x1<x2<1时,0<x1x2<1,1-
| 1 |
| x1x2 |
∴f(x1)-f(x2)>0即f(x1)>f(x2),
∴f(x)在区间(0,1)上是减函数;
②当-1<x1<x2<0时,0<x1x2<1,1-
| 1 |
| x1x2 |
∴f(x1)-f(x2)>0即f(x1)>f(x2),
∴f(x)在区间(-1,0)上是减函数;
③当x1<x2<-1时,x1x2>1,1-
| 1 |
| x1x2 |
∴f(x1)-f(x2)<0即f(x1)<f(x2),
∴f(x)在区间(0,1)上是增函数.
∴函数f(x)在区间(-∞,1)上的单调性是:在(-∞,-1)上是增函数;
在(-1,0)和(0,1)上都是减函数;
∵f(x)=x+
| 1 |
| x |
f(-x)=-x+
| 1 |
| -x |
∴f(x)为奇函数,图象关于原点对称,
且函数f(x)在(-∞,-1),(1,+∞)上递增,在(-1,0),(0,1)上递减
故图象如图所示:

点评:本题主要考查了函数的单调性的定义在证明函数的单调性中的应用,画出函数的图象的关键是熟练应用函数的性质.

练习册系列答案
相关题目
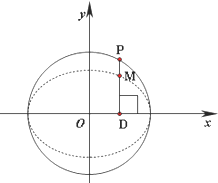 如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且
如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且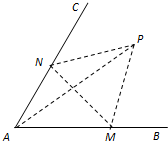 如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
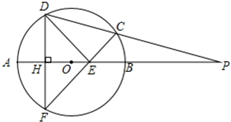 如图,P是⊙O的直径AB延长线上一点,割线PCD交⊙O于C、D两点,弦DF与直径AB垂直,H为垂足,CF与AB交于点E.
如图,P是⊙O的直径AB延长线上一点,割线PCD交⊙O于C、D两点,弦DF与直径AB垂直,H为垂足,CF与AB交于点E.