题目内容

若关于x的方程x2+2x+m=0在-1≤x≤1内有解，求实数m的取值范围．
考点：二次函数的性质
专题：函数的性质及应用,不等式的解法及应用
分析：关于x的方程x2+2x+m=0在-1≤x≤1内有解，即y=x2+2x+m与x轴在-1≤x≤1内有交点．根据函数的图象与性质列不等式组解答．
解答： 解：关于x的方程x2+2x+m=0在-1≤x≤1内有解，
即y=x2+2x+m与x轴在-1≤x≤1内有交点，
∵二次函数函数y的对称轴为x=-1，且开口向上，
∴满足
f(-1)≤0
f(1)≥0
，
即
m-1≤1
m+3≥0
，
解得-3≤m≤1；
∴实数m的取值范围是{m|-3≤m≤1}．
点评：本题考查了二次函数与x轴的交点与方程根的关系问题，解题时结合函数图象列出不等式组，得出答案．
练习册系列答案
相关题目
已知椭圆C的中心在原点O，焦点在x轴上，短轴长为2，离心率为
2
2
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l：y=kx+m与椭圆C有两个不同的交点A，B，且直线OA，OB的斜率之积为
1
2
，问是否存在直线l，使△AOB的面积的值为
2
2
？若存在，求直线的方程，若不存在，请说明理由．
在正数数列{an}中，Sn为an的前n项和，若点（an，Sn）在函数y=
c2-x
c-1
的图象上，其中c为正常数，且c≠1．
（1）求数列{an}的通项公式；
（2）设数列{bn}满足bn=
n2 nan+2
2n+1
，当c=2的时候，是否存在正整数m、n（1＜m＜n），使得b1，bm，bn成等比数列？若存在，求出所有的m、n的值，若不存在，请说明理由；
（3）设数列{cn}满足cn=
n，n=2k-1
2an，n=2k
，k∈N*，当c=
3
3
时候，在数列{cn}中，是否存在连续的三项cr，cr+1，cr+2，按原来的顺序成等差数列？若存在，求出所有满足条件的正整数r的值；若不存在，说明理由．
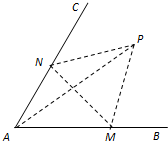如图，经过村庄A有两条夹角为60°的公路AB，AC，根据规划拟在两条公路之间的区域内建一工厂P，分别在两条公路边上建两个仓库M、N （异于村庄A），要求PM=PN=MN=2（单位：千米）．如何设计，使得工厂产生的噪声对居民的影响最小（即工厂与村庄的距离最远）．
若不等式（m-1）x2+（m-1）x+2＞0的解集是R，求m的取值范围．
某程序框图如图所示，则该程序运行后输出S的值是
 
．
已知空间四边形OABC，其对角线为OB，AC，M，N分别是对边OA，BC的中点，点G在线段MN上，且
MG
=2
GN
，现用基组{
OA
，
OB
，
OC
}表示向量
OG
，有
OG
=x
OA
+y
OB
+z
OC
，则x，y，z的值分别为
 
．
若实数x，y满足约束条件：
x≤1
y≤2
2x+y-2≥0
，则z=x+2y的最大值等于
 
．
执行如图的程序框图，则输出的S是（　　）
A、5040B、2450
C、4850D、2550

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网