Question

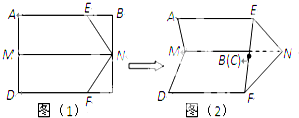如图（1），矩形ABCD中，M、N分别为边AD、BC的中点，E、F分别为边AB、CD上的定点且满足EB=FC，现沿MN，EN，FN折叠使点B、C重合且与E、F共线，如图（2）．若此时二面角A-MN-D的大小为60°，则折叠后EN与平面MNFD所成角的正弦值是（　　）

• A、

  10

  2

• B、

  10

  5

• C、

  15

  5

• D、

  15

  3

Answer 1

考点：直线与平面所成的角

专题：空间角

分析：过E作EQ∥AM交MN于Q，连接FQ，则∠EQF是二面角A-MN-D所成角的平面角，取FQ的中点H，连接EH，HN，则EH⊥平面MNFD，则∠ENH是EN与平面MNFD所成角，由此能求出折叠后EN与平面MNFD所成角的正弦值．

解答： 解：过E作EQ∥AM交MN于Q，连接FQ，
则EQ⊥MN，FQ⊥MN，
∴∠EQF是二面角A-MN-D所成角的平面角，
∴∠EQF=60°，∴△EQF为等边三角形，
设EQ=a，则FQ=EF=a，
∴平面EQF⊥平面MNFD，
取FQ的中点H，连接EH，HN，
则EH⊥平面MNFD，∴∠ENH是EN与平面MNFD所成角，
∵EN=

5

2

a，EH=

3

2

a，
∴sin∠ENF=

15

3

．
故选：D．

点评：本题考查线面角正弦值的求法，是中档题，解题时要注意空间思维能力的培养．