题目内容
已知关于x的方程x2+2px+(2-q2)=0(p,q∈R)有两个相等的实根,则p+q的取值范围是( )
| A、[-2,2] | ||||
| B、(-2,2) | ||||
C、[-
| ||||
D、(-
|
考点:二次函数的性质
专题:
分析:根据已知条件容易得到p2+q2=2,所以可设p=
sinθ,q=
cosθ,所以可得到p+q=2sin(θ+
),所以-2≤p+q≤2.
| 2 |
| 2 |
| π |
| 4 |
解答:
解:由已知条件△=4p2-4(2-q2)=0;
∴p2+q2=2;
∴(
)2+(
)2=1;
∴设
=sinθ,
=cosθ,θ∈R;
∴p=
sinθ,q=
cosθ;
∴p+q=2(
sinθ+
cosθ)=2sin(θ+
);
∴-2≤p+q≤2;
∴p+q的取值范围是[-2,2].
故选A.
∴p2+q2=2;
∴(
| p | ||
|
| q | ||
|
∴设
| p | ||
|
| q | ||
|
∴p=
| 2 |
| 2 |
∴p+q=2(
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
∴-2≤p+q≤2;
∴p+q的取值范围是[-2,2].
故选A.
点评:考查一元二次方程有两个相等实根时判别式△的取值情况,以及sin2θ+cos2θ=1的运用,换元的方法.

练习册系列答案
相关题目
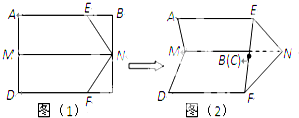 如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )
如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )