题目内容
已知顶点在原点，焦点在x轴的负半轴的抛物线截直线y=x+
所得的弦长|P1P2|=4
，求此抛物线的方程．
| 3 |
| 2 |
| 2 |
考点：抛物线的标准方程
专题：圆锥曲线中的最值与范围问题
分析：抛物线y2=2px，p＜0，联立
，得x2+（3-2p）x+
=0，由此利用韦达定理，结合已知条件能注出抛物线方程．
|
| 9 |
| 4 |
解答：
解：抛物线y2=2px，p＜0，直线y=x+
，联立
，得x2+（3-2p）x+
=0，
根据韦达定理有x1+x2=2p-3，x1x2=
，
|P1P2|=4
，|P1P2|2=32，
∴（x1-x2）2+（y1-y2）2=32，
由直线方程，得y1-y2=x1-x2，
∴（x1-x2）2+（x1-x2）2=32，∴（x1-x2）2=16，
∴（x1+x2）2-4x1x2=16，∴（2p-3）2-9=16，
∴（2p-3）2=25，p＜0，∴2p-3=-5，解得p=-1，
∴抛物线方程为y2=-2x．
| 3 |
| 2 |
|
| 9 |
| 4 |
根据韦达定理有x1+x2=2p-3，x1x2=
| 9 |
| 4 |
|P1P2|=4
| 2 |
∴（x1-x2）2+（y1-y2）2=32，
由直线方程，得y1-y2=x1-x2，
∴（x1-x2）2+（x1-x2）2=32，∴（x1-x2）2=16，
∴（x1+x2）2-4x1x2=16，∴（2p-3）2-9=16，
∴（2p-3）2=25，p＜0，∴2p-3=-5，解得p=-1，
∴抛物线方程为y2=-2x．
点评：本题考查抛物线方程的求法，是中档题，解题时要认真审题，注意函数与方程思想的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
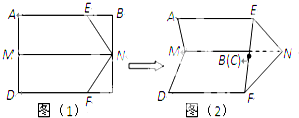如图（1），矩形ABCD中，M、N分别为边AD、BC的中点，E、F分别为边AB、CD上的定点且满足EB=FC，现沿MN，EN，FN折叠使点B、C重合且与E、F共线，如图（2）．若此时二面角A-MN-D的大小为60°，则折叠后EN与平面MNFD所成角的正弦值是（ ）