题目内容
已知A,B,C的坐标分别为A(3,0),B(0,3),C(cosα,sinα),D(sinβ,0),α∈(
,
),β∈(-
,
).
(1)若
⊥
,求
的值
(2)若|
|=|
|,又
在
上投影为
,求cos(α-β)的值.
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(1)若
. |
| AC |
. |
| BC |
| 2sin2α+sin2α |
| 1+tanα |
(2)若|
| AC |
| BC |
. |
| AD |
. |
| AB |
4
| ||
| 3 |
考点:平面向量数量积的运算
专题:计算题,三角函数的求值,平面向量及应用
分析:(1)运用向量垂直的条件,即为数量积为0,结合二倍角公式和同角公式,化简即可得到;
(2)运用向量模的公式和向量的投影概念,得到α,β的正弦和余弦,再由两角差的余弦公式计算即可得到.
(2)运用向量模的公式和向量的投影概念,得到α,β的正弦和余弦,再由两角差的余弦公式计算即可得到.
解答:
解:(1)由于A(3,0),B(0,3),C(cosα,sinα),
则
=(cosα-3,sinα),
=(cosα,sinα-3),
若
⊥
,则cosα(cosα-3)+sinα(sinα-3)=0,
化简可得,cosα+sinα=
,α∈(
,π).
平方可得,1+2sinαcosα=
,
即有2sinαcosα=-
.
则
=
=2sinαcosα=-
;
(2)若|
|=|
|,则(cosα-3)2+sin2α=cos2α+(sinα-3)2,
化简可得,sinα=cosα,即tanα=1,
由α∈(
,
),则α=
.
=(-3,3),
=(sinβ-3,0)
则
在
上投影为
=
=
,
即有sinβ=
,
由于β∈(-
,
),则cosβ=
=
,
则cos(α-β)=cosαcosβ+sinαsinβ=-
×
+(-
)×
=-
.
则
| AC |
| BC |
若
. |
| AC |
. |
| BC |
化简可得,cosα+sinα=
| 1 |
| 3 |
| π |
| 2 |
平方可得,1+2sinαcosα=
| 1 |
| 9 |
即有2sinαcosα=-
| 8 |
| 9 |
则
| 2sin2α+sin2α |
| 1+tanα |
| 2sin2α+2sinαcosα | ||
1+
|
| 8 |
| 9 |
(2)若|
| AC |
| BC |
化简可得,sinα=cosα,即tanα=1,
由α∈(
| π |
| 2 |
| 3π |
| 2 |
| 5π |
| 4 |
| AB |
| AD |
则
. |
| AD |
. |
| AB |
| ||||
|
|
| 3(3-sinβ) | ||
3
|
4
| ||
| 3 |
即有sinβ=
| 1 |
| 3 |
由于β∈(-
| π |
| 2 |
| π |
| 2 |
1-
|
2
| ||
| 3 |
则cos(α-β)=cosαcosβ+sinαsinβ=-
| ||
| 2 |
2
| ||
| 3 |
| ||
| 2 |
| 1 |
| 3 |
=-
4+
| ||
| 6 |
点评:本题考查平面向量的数量积的坐标表示,考查向量垂直的条件和向量的投影的定义,考查三角函数的恒等变换公式的运用:化简和求值,考察运算能力,属于中档题.

练习册系列答案
相关题目
四面体ABCD中,AD=BC,且AD⊥BC,E、F分别是AB、CD的中点,则EF与BC所成的角为( )
| A、30° | B、45° |
| C、60° | D、90° |
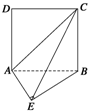 如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )
如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )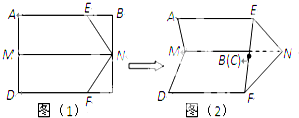 如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )
如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )